Find the difference between radii of smaller and larger circles, whose centers lie on the circle ${x^2} + {y^2} + 4x - 6y - 23 = 0$ and pass through the point (5, 12).
A)8
B)9
C)10
D)11
E)12
Answer
Verified361.5k+ views
Hint: General equation of the circle is ${x^2} + {y^2} + 2gx + 2fy + c = 0$, with center of the circle lies on (-g, -f) and radius of the circle is equal to $\sqrt {{g^2} + {f^2} - c} $.
Complete step-by-step answer:
The given circle equation is $${x^2} + {y^2} + 4x - 6y - 23 = 0$$.
Let R be the radius of the above circle.
Comparing the given equation with general equation of the circle we will get g = 2, f = -3, c = -23
$ \Rightarrow $Center of the circle (-g, -f) = (2, -3)
$ \Rightarrow $ The radius of the circle = $\sqrt {{g^2} + {f^2} - c} = \sqrt {{2^2} + {{( - 3)}^2} - ( - 23)} = \sqrt {36} $
$ \Rightarrow $ Radius of the circle R = 6 units.
The geometrical representation of the circle looks similar to the below figure with center at (2, -3) and radius R = 6 units.
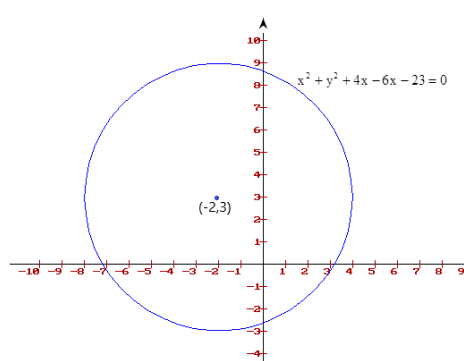
Now, we have to draw two circles from the point (5, 12) on a condition that those two circles must have a center lying on the circle $${x^2} + {y^2} + 4x - 6y - 23 = 0$$. And one circle with minimum possible radius and another circle with maximum possible radius satisfying the above condition.
When we draw those two circles it will be similar to the below figure.
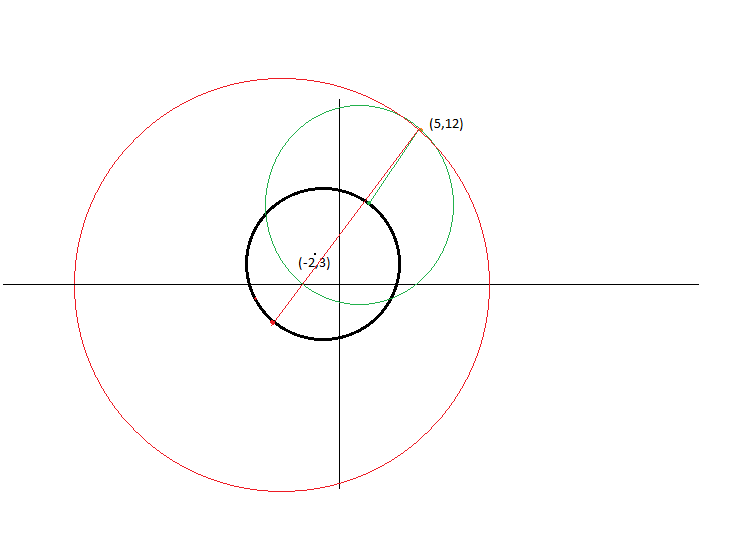
[Black circle is the circle with equation$${x^2} + {y^2} + 4x - 6y - 23 = 0$$.
Green color circle represents the smallest possible circle passing through (5, 12) point and its center lies on the black circle.
Red color circle represents the largest possible circle passing through (5, 12) point and its center lies on the black circle.]
We have to find the difference between radii of those largest and smallest circles.
If we observe the figure above it is clear that the difference in radii of green and red circles is equal to the diameter of the black circle.
$ \Rightarrow $ Difference = 2R = 2(6) = 12 units.
Option E is the correct answer.
$\therefore $ The difference between radii of smaller and larger circles, whose centers lie on the circle ${x^2} + {y^2} + 4x - 6y - 23 = 0$ and pass through the point (5, 12) = 12 units
Note: Whenever we encounter these kinds of problems we first have to understand the question clearly. Then we have to picturize the given information to get the logic behind it, so that we can easily solve the problem.
Complete step-by-step answer:
The given circle equation is $${x^2} + {y^2} + 4x - 6y - 23 = 0$$.
Let R be the radius of the above circle.
Comparing the given equation with general equation of the circle we will get g = 2, f = -3, c = -23
$ \Rightarrow $Center of the circle (-g, -f) = (2, -3)
$ \Rightarrow $ The radius of the circle = $\sqrt {{g^2} + {f^2} - c} = \sqrt {{2^2} + {{( - 3)}^2} - ( - 23)} = \sqrt {36} $
$ \Rightarrow $ Radius of the circle R = 6 units.
The geometrical representation of the circle looks similar to the below figure with center at (2, -3) and radius R = 6 units.
Now, we have to draw two circles from the point (5, 12) on a condition that those two circles must have a center lying on the circle $${x^2} + {y^2} + 4x - 6y - 23 = 0$$. And one circle with minimum possible radius and another circle with maximum possible radius satisfying the above condition.
When we draw those two circles it will be similar to the below figure.
[Black circle is the circle with equation$${x^2} + {y^2} + 4x - 6y - 23 = 0$$.
Green color circle represents the smallest possible circle passing through (5, 12) point and its center lies on the black circle.
Red color circle represents the largest possible circle passing through (5, 12) point and its center lies on the black circle.]
We have to find the difference between radii of those largest and smallest circles.
If we observe the figure above it is clear that the difference in radii of green and red circles is equal to the diameter of the black circle.
$ \Rightarrow $ Difference = 2R = 2(6) = 12 units.
Option E is the correct answer.
$\therefore $ The difference between radii of smaller and larger circles, whose centers lie on the circle ${x^2} + {y^2} + 4x - 6y - 23 = 0$ and pass through the point (5, 12) = 12 units
Note: Whenever we encounter these kinds of problems we first have to understand the question clearly. Then we have to picturize the given information to get the logic behind it, so that we can easily solve the problem.
Last updated date: 22nd Sep 2023
•
Total views: 361.5k
•
Views today: 4.61k
