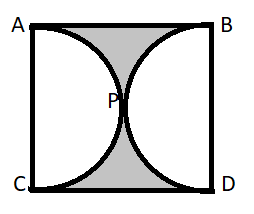
Find the area of the shaded region in the fig., if ABCD is a square of side 14cm and APC and BPD are semicircles.
Answer
Verified362.7k+ views
Hint:- The side length of the square is equal to the diameter of the semicircle.
Given , the side length of the square is 14cm. Now, the shaded region as well as the semicircles are inside the square. Hence, the total area will comprise the area of the shaded region and the semicircles.
i.e.
${\text{Area of square = area of semicircle APC + area of shaded region + area of semicircle BPD}}$ -(1)
The area of the square is equal to \[{({\text{side length)}}^2}\] .
Area of Square ABCD $ = {\text{ }}{\left( {14{\text{cm}}} \right)^2}$
${\text{ = 196 c}}{{\text{m}}^2}$ -(2)
Now, the semicircles APC and BPD.
Side AC = diameter of the semicircle APC = diameter of the semicircle BPD
Area of semicircle = $\dfrac{\pi }{8} \times {\left( {{\text{diameter}}} \right)^2}$
Area of semicircle APC =$\dfrac{\pi }{8} \times {\left( {14{\text{cm}}} \right)^2}$
Taking $\pi $ = 3.141, we get
Area of semicircle APC = $76.97{\text{ c}}{{\text{m}}^2}$ -(3)
As the diameter of semicircle APC and BPD are equal, the area will also be equal.
So, area of semicircle BPD = $76.97{\text{ c}}{{\text{m}}^2}$ -(4)
Putting the values of areas of square and semi circles from equations (2),(3) and (4) into equation (1).We get,
$
\Rightarrow 196{\text{ = 76}}{\text{.97 + area of shaded region + 76}}{\text{.97}} \\
\Rightarrow {\text{area of shaded region = 196 - 76}}{\text{.97 - 76}}{\text{.97}} \\
{\text{ = 42}}{\text{.06 c}}{{\text{m}}^2} \\
$
So, the answer is 42.06 square cm.
Note:- In these types of questions, for finding the solution a basic relation is considered i.e. outer area is equated to sum of the area’s of inner portions. Always remember to make sure that the area of each portion is present in the same square unit.
Given , the side length of the square is 14cm. Now, the shaded region as well as the semicircles are inside the square. Hence, the total area will comprise the area of the shaded region and the semicircles.
i.e.
${\text{Area of square = area of semicircle APC + area of shaded region + area of semicircle BPD}}$ -(1)
The area of the square is equal to \[{({\text{side length)}}^2}\] .
Area of Square ABCD $ = {\text{ }}{\left( {14{\text{cm}}} \right)^2}$
${\text{ = 196 c}}{{\text{m}}^2}$ -(2)
Now, the semicircles APC and BPD.
Side AC = diameter of the semicircle APC = diameter of the semicircle BPD
Area of semicircle = $\dfrac{\pi }{8} \times {\left( {{\text{diameter}}} \right)^2}$
Area of semicircle APC =$\dfrac{\pi }{8} \times {\left( {14{\text{cm}}} \right)^2}$
Taking $\pi $ = 3.141, we get
Area of semicircle APC = $76.97{\text{ c}}{{\text{m}}^2}$ -(3)
As the diameter of semicircle APC and BPD are equal, the area will also be equal.
So, area of semicircle BPD = $76.97{\text{ c}}{{\text{m}}^2}$ -(4)
Putting the values of areas of square and semi circles from equations (2),(3) and (4) into equation (1).We get,
$
\Rightarrow 196{\text{ = 76}}{\text{.97 + area of shaded region + 76}}{\text{.97}} \\
\Rightarrow {\text{area of shaded region = 196 - 76}}{\text{.97 - 76}}{\text{.97}} \\
{\text{ = 42}}{\text{.06 c}}{{\text{m}}^2} \\
$
So, the answer is 42.06 square cm.
Note:- In these types of questions, for finding the solution a basic relation is considered i.e. outer area is equated to sum of the area’s of inner portions. Always remember to make sure that the area of each portion is present in the same square unit.
Last updated date: 26th Sep 2023
•
Total views: 362.7k
•
Views today: 5.62k
