Question

Find the area of cardioids \[r=a\left( 1+\cos \theta \right)\].

Answer 1

Hint: First try to make a rough sketch. Now, break the entire area into parts based on symmetry. Thus, break the integral up into two smaller intervals by looking at the diagram and proceed.

Complete step-by-step answer:
A cardioid is a mathematically generated shape resembling a heart or half an apple. Constructing cardioids on a polar graph is done using equations.
The given cardioids can be graphically represented as

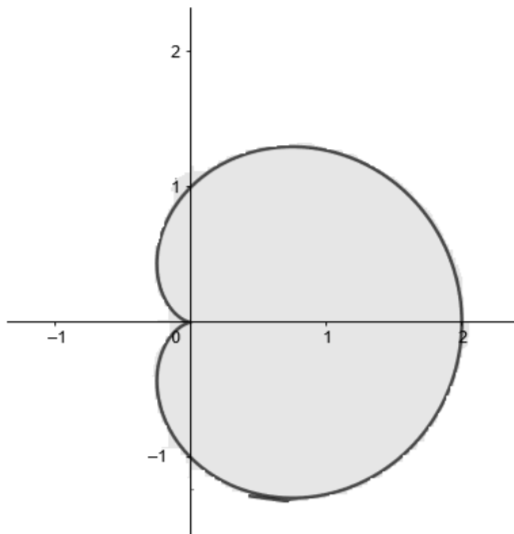
The shaded region is the required area.
The area of a polar curve is given by the formula
\[\text{Area}=\int\limits_{0}^{\pi }{\dfrac{1}{2}{{r}^{2}}d\theta }\]
Note that the above area is only for the region above x-axis.
From the graph, we can see that the curve is symmetrical around x-axis and also the area above and below the x-axis is equal, so the total area will be,
Total Area \[=2\int\limits_{0}^{\pi }{\dfrac{1}{2}{{r}^{2}}d\theta }\]
Taking out the constant term, we get
Total Area \[=2\times \dfrac{1}{2}\int\limits_{0}^{\pi }{{{r}^{2}}d\theta }\]
Cancelling the like terms, we get
Total Area \[=\int\limits_{0}^{\pi }{{{r}^{2}}d\theta }\]
Substituting the given equation of cardioids, we get
Total area \[=\int\limits_{0}^{\pi }{{{a}^{2}}{{\left( 1+\cos \theta \right)}^{2}}d\theta }\]
Now taking out the constant term, we get
Total area \[={{a}^{2}}\int\limits_{0}^{\pi }{{{\left( 1+\cos \theta \right)}^{2}}d\theta }\]
We know the formula, ${{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$ , applying this in the above equation, we get
Total area \[={{a}^{2}}\int\limits_{0}^{\pi }{\left( 1+{{\cos }^{2}}\theta +2\cos \theta \right)d\theta }\]
We know \[{{\cos }^{2}}\theta =\dfrac{1}{2}\left( 1+\cos 2\theta \right)\], substituting this value in above equation, we get
Total area \[={{a}^{2}}\int\limits_{0}^{\pi }{\left( 1+\dfrac{1}{2}\left( 1+\cos 2\theta \right)+2\cos \theta \right)d\theta }\]
Taking the LCM, we get
Total area \[={{a}^{2}}\int\limits_{0}^{\pi }{\left( \dfrac{2+\left( 1+\cos 2\theta \right)+4\cos \theta }{2} \right)d\theta }\]
Taking out the constant term, we get
Total area \[=\dfrac{{{a}^{2}}}{2}\int\limits_{0}^{\pi }{\left( 3+\cos 2\theta +4\cos \theta \right)d\theta }\]
Now we know the integration of sum of functions is sum of individual integration of the functions, i.e.,
Total area \[=\dfrac{{{a}^{2}}}{2}\left[ \int\limits_{0}^{\pi }{\left( 3 \right)d\theta }+\int\limits_{0}^{\pi }{\left( \cos 2\theta \right)d\theta }+\int\limits_{0}^{\pi }{\left( 4\cos \theta \right)d\theta } \right]\]
We know integration of $\cos x$ is $\sin x$ , so the above equation becomes,
Total area \[=\dfrac{{{a}^{2}}}{2}\left[ \left[ 3\theta \right]_{0}^{\pi }+\left[ \dfrac{\sin 2\theta }{2} \right]_{0}^{\pi }+\left[ 4\sin \theta \right]_{0}^{\pi } \right]\]
Applying the limits, we get
Total area \[=\dfrac{{{a}^{2}}}{2}\left[ \left[ 3\pi -3(0) \right]+\left[ \dfrac{\sin 2(\pi )}{2}-\dfrac{\sin 2(0)}{2} \right]+\left[ 4\sin (\pi )-4\sin (0) \right] \right]\]
We know, $\sin 0=\sin \pi =0$ , so the above equation becomes,
Total area \[=\dfrac{{{a}^{2}}}{2}\left[ \left[ 3\pi -0 \right]+\left[ (0)-0 \right]+\left[ (0)-0 \right] \right]\]
Therefore, total area \[=\dfrac{3\pi {{a}^{2}}}{2}\]sq.units.
So, the area of cardioid is \[\dfrac{3}{2}\pi {{a}^{2}}\] sq. units.

Note: The possibility of mistake is that the area given by\[\int\limits_{0}^{\pi }{\dfrac{1}{2}{{r}^{2}}d\theta }\] is not doubled and only half the area is calculated.
Another possibility is taking integration of $\cos \theta $ is $-\sin \theta $, which is wrong. This is true in case of differentiation, i.e.,
$\begin{align}
  & \dfrac{d}{d\theta }(\cos \theta )=-\sin \theta \\
 & \int{\cos \theta d\theta }=\sin \theta \\
\end{align}$