Question

Find the area of a triangle whose perimeter is 22 cm, one side is 9 cm and the difference of the other two sides is 3 cm.

Answer 1

Hint: Let the sides of the triangle be x, y, and z. Express the given conditions using these variables and solve the system of equations thus obtained simultaneously. Compute the semi-perimeter of the triangle and use the lengths of the sides and the semi-perimeter to calculate the area of the triangle using the formula: $\sqrt {s(s - a)(s - b)(s - c)} $ where $s = \dfrac{{a + b + c}}{2}$ is the semi-perimeter of the triangle.

Complete step by step answer:
Let us write down all the given information one by one.
Perimeter of the given triangle = 22 cm
Length of one of the sides of the triangle = 9 cm
Difference between the remaining two sides = 3 cm.
We are asked to find the area of the triangle with the above characteristics.

If we use variables to express the above information, we would get a system of equations.
So, let’s do that.
Let the lengths of the sides of the triangle be denoted by x, y, and z.
Now, we will rewrite the given information using the variables x, y, and z.
Perimeter of the triangle is the sum of all lengths of the sides of the triangle.
Therefore, we have \[x + y + z = 22 \ldots \ldots \ldots \ldots \ldots \left( 1 \right)\]

Let x = 9 cm. Also, let y be greater than z.
Then \[y - z = 3 \ldots \ldots \ldots \ldots \ldots \ldots \ldots \left( 2 \right)\]
Substitute for x in (1).
\[9 + y + z = 22\]
Therefore, \[y + z = 22 - 9 = 13 \ldots \ldots \ldots \ldots \ldots \left( 3 \right)\]
Add (2) and (3), we get \[2y = 16\]
Therefore, y = 8 cm.
Now, substitute for x and y in (1).
Then, we get
\[
  x + y + z = 22 \\
   \Rightarrow 9 + 8 + z = 22 \\
   \Rightarrow 17 + z = 22 \\
   \Rightarrow z = 22 - 17 \\
   \Rightarrow z = 5 \\
 \]
Therefore, z = 5 cm.
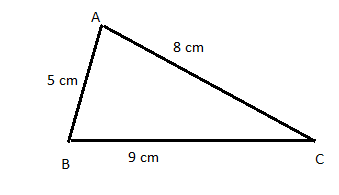
Thus, we have the lengths of the sides of the triangle: 5 cm, 8 cm, 9 cm.
If lengths of the sides of a triangle denoted by a, b, c are known, then we can compute the area of the triangle using the formula: $\sqrt {s(s - a)(s - b)(s - c)} $ where $s = \dfrac{{a + b + c}}{2}$ is the semi-perimeter of the triangle.
Now, we have the perimeter of the triangle = 22 cm.
Therefore, \[s = 22 \div 2 = 11\]
Also, here a = 5, b = 8, c = 9
The triangle will look like the following figure:

Thus, the area of the triangle$ = \sqrt {s(s - a)(s - b)(s - c)} $
$
   = \sqrt {11(11 - 5)(11 - 8)(11 - 9)} \\
   = \sqrt {11(6)(3)(2)} \\
   = 6\sqrt {11} \\
 $

Hence we get the area of the triangle as $6\sqrt {11} $\,sq. cm.

Note: A common mistake students often make while finding the area using the formula $\sqrt {s(s - a)(s - b)(s - c)} $where $s = \dfrac{{a + b + c}}{2}$ is that they forget to divide the perimeter by 2 to find the value of s. This needs to be avoided to get the correct answer.