Questions & Answers
Question
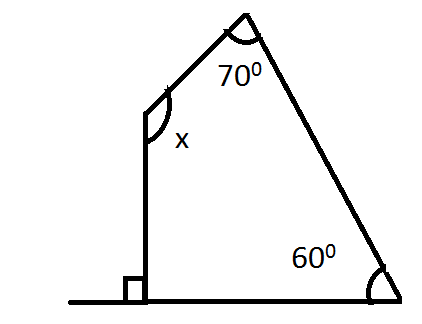
AnswersFind the angle measure x in the following figure?
Answer
Verified129.9k+ views
Hint: The Quadrilateral or quadrangle is a shape with four sides. to be considered as a quadrangle. the shape must
1) Have four straight sides
2) Be a flat shape (2dimentional)
3) Be a closed figure.
4) Edges and vertices \[ = {\text{ }}4\]
The word quadrilateral is derived from the Latin word quadric, a variant of four sides and the latus meaning side quadrilateral are either convex or concave.
The interior angle of a simple quadrilateral ABCD adds up to \[{360^0}\;\]arc.
i.e. \[\angle A + {\text{ }}\angle {\text{ }}B{\text{ }} + {\text{ }}\angle {\text{ }}C{\text{ }} + {\text{ }}\angle {\text{ }}D = {\text{ }}{360^0}\].
Any quadrilateral that is not self-intersecting is a simple quadrilateral
Trapezium, Isosceles trapezium Parallelogram, Rhombus, Rhomboid Rectangle, Square, oblong, Kite tangential Quadrilateral, Tangent of trapezoid, cyclic Quadrilateral, Right Kite, Harmonic Quadrilate Bicentric Quadrilateral, Orthodiagonal, Oceadrilateral, Equidiagonal Quadrilateral are all different type of Quarilaterlas.
Complete step by step answer:
According to the question, there are 4 Angles in a Quadrilateral.
Let\[\angle {\text{ }}A = 90,{\text{ }}\angle {\text{ }}B = {\text{ }}x,{\text{ }}\angle {\text{ }}C = {\text{ }}70,\angle {\text{ }}D = {\text{ }}60\].
Since in quadrilateral sum of interior angles is equal to 3600.
\[\angle {\text{ }}A{\text{ }} + {\text{ }}\angle {\text{ }}B{\text{ }} + {\text{ }}\angle {\text{ }}C{\text{ }} + {\text{ }}\angle {\text{ }}D = {360^0}\]
\[90 + {\text{ }}x{\text{ }} + {\text{ }}70{\text{ }} + {\text{ }}60{\text{ }} = {360^0}\]
\[\;\left( {90{\text{ }} + {\text{ }}60} \right){\text{ }} + {\text{ }}x{\text{ }} = {\text{ }}360{\text{ }} - 70\]
\[150{\text{ }} + {\text{ }}x{\text{ }} = 290\]
\[x{\text{ }} = {\text{ }}290{\text{ }}-{\text{ }}150\]
\[x{\text{ }} = {\text{ }}140\]
\[\angle {\text{ }}B = 140\]
Note: A quadrilateral is a shape of \[4\] sides for which any quadrilateral we draw a diagonal line to divide it into two triangles. Each triangle has an angle sum of \[180\]degree.
Therefore, the total angle sum of a quadrilateral is\[360\]. A quadrilateral cannot have \[3\] Obtuse angle where an obtuse angle is an angle that has a measure that is greater than\[{90^0}\].
1) Have four straight sides
2) Be a flat shape (2dimentional)
3) Be a closed figure.
4) Edges and vertices \[ = {\text{ }}4\]
The word quadrilateral is derived from the Latin word quadric, a variant of four sides and the latus meaning side quadrilateral are either convex or concave.
The interior angle of a simple quadrilateral ABCD adds up to \[{360^0}\;\]arc.
i.e. \[\angle A + {\text{ }}\angle {\text{ }}B{\text{ }} + {\text{ }}\angle {\text{ }}C{\text{ }} + {\text{ }}\angle {\text{ }}D = {\text{ }}{360^0}\].
Any quadrilateral that is not self-intersecting is a simple quadrilateral
Trapezium, Isosceles trapezium Parallelogram, Rhombus, Rhomboid Rectangle, Square, oblong, Kite tangential Quadrilateral, Tangent of trapezoid, cyclic Quadrilateral, Right Kite, Harmonic Quadrilate Bicentric Quadrilateral, Orthodiagonal, Oceadrilateral, Equidiagonal Quadrilateral are all different type of Quarilaterlas.
Complete step by step answer:
According to the question, there are 4 Angles in a Quadrilateral.
Let\[\angle {\text{ }}A = 90,{\text{ }}\angle {\text{ }}B = {\text{ }}x,{\text{ }}\angle {\text{ }}C = {\text{ }}70,\angle {\text{ }}D = {\text{ }}60\].
Since in quadrilateral sum of interior angles is equal to 3600.
\[\angle {\text{ }}A{\text{ }} + {\text{ }}\angle {\text{ }}B{\text{ }} + {\text{ }}\angle {\text{ }}C{\text{ }} + {\text{ }}\angle {\text{ }}D = {360^0}\]
\[90 + {\text{ }}x{\text{ }} + {\text{ }}70{\text{ }} + {\text{ }}60{\text{ }} = {360^0}\]
\[\;\left( {90{\text{ }} + {\text{ }}60} \right){\text{ }} + {\text{ }}x{\text{ }} = {\text{ }}360{\text{ }} - 70\]
\[150{\text{ }} + {\text{ }}x{\text{ }} = 290\]
\[x{\text{ }} = {\text{ }}290{\text{ }}-{\text{ }}150\]
\[x{\text{ }} = {\text{ }}140\]
\[\angle {\text{ }}B = 140\]
Note: A quadrilateral is a shape of \[4\] sides for which any quadrilateral we draw a diagonal line to divide it into two triangles. Each triangle has an angle sum of \[180\]degree.
Therefore, the total angle sum of a quadrilateral is\[360\]. A quadrilateral cannot have \[3\] Obtuse angle where an obtuse angle is an angle that has a measure that is greater than\[{90^0}\].