Question

Find the angle in radian through which a pendulum swings if its length is 75 cm and the tip describes an arc of length
(i) 10 cm.
(ii) 15 cm.
(iii) 21 cm.

Answer 1

Hint: To solve this question, we will use some basic points of radian measure. If in a circle of radius r, an arc of length l and subtends an angle $\theta$ radian at the centre, then we have $\theta =\dfrac{l}{r}$ or $l = r \theta$.

Complete step-by-step answer:

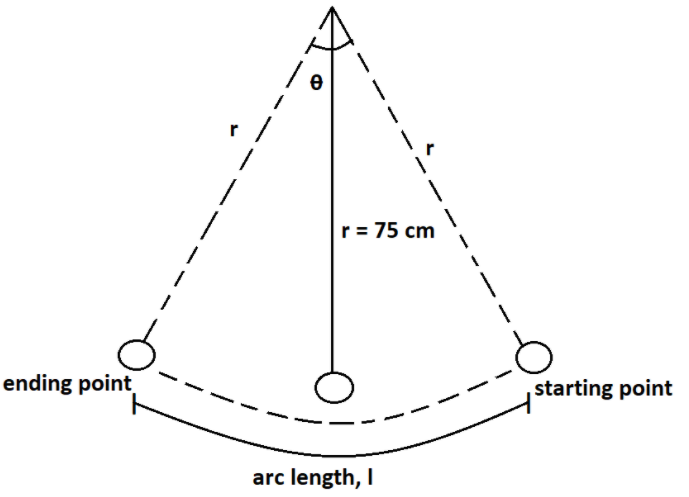
Given that,
The length of the pendulum, $r = 75$ cm.
Here, we have to find the angle for the given length of the arc.
(i) arc length, $ l = 10$ cm.
We know that,
$\theta = \dfrac{l}{r}$,
Putting all the given values, we will get
$ \Rightarrow \theta = \dfrac{10cm}{75}$
$ \Rightarrow \theta = \dfrac{2}{15}$ radian.
(ii) arc length, $l = 15$ cm.
We have,
$\theta =\dfrac{l}{r}$,
Putting all the given values, we will get
$ \Rightarrow \theta =\dfrac{{15cm}}{{75}}$
$ \Rightarrow \theta =\dfrac{1}{5}$ radian.
(iii) arc length, $l = 21$ cm.
We have,
$\theta =\dfrac{l}{r}$,
Putting the values, we will get
$ \Rightarrow \theta = \dfrac{{21cm}}{{75}}$
$ \Rightarrow \theta =\dfrac{7}{{25}}$ radian

Note: Whenever we ask this type of question, we have to remember the method of finding the angle subtended by an arc at the center of a circle with radius. We will use the required formula and by putting all the values in the formula for each case, we will get the required answer. Since angles are measured either in degree or in radians, we choose the convention that whatever we write angle \[{\theta}^0 \], we mean the angle whose degree measure is $\theta$ and whatever we write angle $\beta $, we mean the angle whose radian measure is $\beta $. The conversion of radian measure in degree measure and degree measure in radian measure can be done by using the following formula:
$ \Rightarrow $ Radian measure = $\dfrac{\pi }{{180}} \times $ degree measure.
$ \Rightarrow $ Degree measure = $\dfrac{{180}}{\pi } \times $ radian measure.