Question

Find equation of circle, one of whose diameter is the latus rectum \[{Y^2} = {\text{ }}4{\text{ }}ax\]. Show that the circle goes through the common point of the axis and the directrix of parabola.

Answer 1

Hint: This question has to be solved with the help of general formulas of parabola\[{Y^2} = {\text{ }}4{\text{ }}ax\]
i.e. vertex, directrix, latus rectum , focus, axis.


Complete step by step solution:-

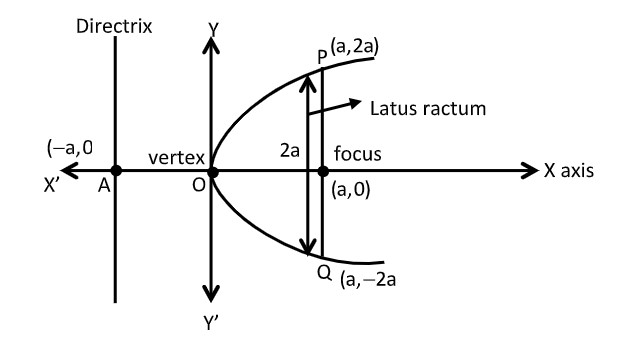
Firstly draw the right hand parabola\[{Y^2} = {\text{ }}4{\text{ }}ax\] as shown in the figure.
As we have to prove that this equation of circle goes through the common point of axis & directrix of parabola i.e. \[A = ( - a,0)\]
As directrix is having ‘a’ distance from the origin in the opposite direction and equation of axis of parabola is \[y{\text{ }} = {\text{ }}0\] as the parabolic curve is symmetrical about y axis.
Since length of diameter is equal to length of latus rectum of \[{y^2} = {\text{ }}4ax\]
So, endpoints of latus Rectum of Parabola endPoints are the points of diameter of circle where PQ represents diameter of circle and latus Rectum of parabola.

\[\begin{array}{*{20}{l}}
  {P = \left( {a,2a} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;Q = (a, - 2a)} \\
  {\left( {{x_1},{\text{ }}{y_1}} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{x_2},{\text{ }}{y_2}} \right)}
\end{array}\]
We know that that if \[2\] endpoints of diameter are given, then equation of circle is
\[\left( {x{\text{ }}-{\text{ }}{x_1}} \right){\text{ }}\left( {x{\text{ }}-{\text{ }}{x_2}} \right){\text{ }} + {\text{ }}\left( {y - {y_1}} \right){\text{ }}\left( {y{\text{ }}-{\text{ }}{y_2}} \right){\text{ }} = {\text{ }}0\]
Here x1 = a, x2 = a
\[{Y_1} = {\text{ }}2a,\;\;\;\;\;\;\;{y_2} = {\text{ }} - 2a\]
Put these values in above equation:
\[\begin{array}{*{20}{l}}
  {\left( {x{\text{ }}-{\text{ }}a} \right){\text{ }}\left( {x{\text{ }}-{\text{ }}a} \right){\text{ }} + {\text{ }}\left( {y{\text{ }}-{\text{ }}2a} \right){\text{ }}(y - \left( { - 2a} \right){\text{ }} = {\text{ }}0} \\
  {{{\left( {x{\text{ }}-{\text{ }}a} \right)}^2} + {\text{ }}\left( {y - 2a} \right){\text{ }}\left( {y + 2a} \right){\text{ }} = {\text{ }}0}
\end{array}\]
\[
  Since{\text{ }}\left( {a + b} \right)\left( {a - b} \right){\text{ }} = {\text{ }}{a^2}-{\text{ }}{b^2} \\
  \;{\left( {x{\text{ }}-{\text{ }}a} \right)^2} + {\text{ }}{\left( y \right)^2}-{\text{ }}{\left( {2a} \right)^2} = {\text{ }}0 \\
  {x^2} + {\text{ }}{a^2}-{\text{ }}2ax{\text{ }} + {\text{ }}{y^2}-{\text{ }}4{a^2} = {\text{ }}0\; \\
  {x^2} + {\text{ }}{y^2}-{\text{ }}2ax{\text{ }}-{\text{ }}3{a^2} = {\text{ }}0{\text{ }} - - - - - - - - - - {\text{ }}\left( 1 \right) \\
 \]
Which is the requisite equation of circle
Now, we know that coordinates of A are \[\left( { - a,{\text{ }}0} \right)\]
Put \[x{\text{ }} = {\text{ }} - {\text{ }}a,{\text{ }}y{\text{ }} = {\text{ }}0\] in equation \[\left( 1 \right)\]
\[
  \begin{array}{*{20}{l}}
  {{{\left( { - a} \right)}^2} + {\text{ }}0{\text{ }}-{\text{ }}2a\left( { - a} \right){\text{ }}3{a^2} = {\text{ }}0} \\
  {{a^2} + {\text{ }}2{a^2}-{\text{ }}3{a^2} = {\text{ }}0} \\
  {3{a^2}-{\text{ }}3{a^2} = {\text{ }}0}
\end{array} \\
  0{\text{ }} = {\text{ }}0 \\
 \]
$\therefore $ Point
\[\left( { - a,{\text{ }}0} \right)\]satisfied the equation of circle \[{x^2} + {\text{ }}{y^2}-{\text{ }}2ax{\text{ }}-{\text{ }}3{a^2} = {\text{ }}0.\] As it is the intersection point of directrix and axis of parabola.

Note: In these types of questions, various types of parabolic equations can be given to us, so we can solve these types of questions according to the type of parabola given to us may be right, left, upward or downward.