
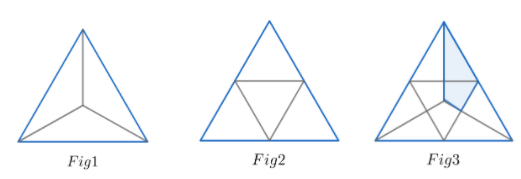
Fig $1$ and Fig $2$ show an equilateral triangle divided into thirds and quarters respectively. They are combined in Fig $3$ . Calculate the fraction of Fig $3$ that is shaded.
$\begin{align}
& \left( A \right)\dfrac{7}{12} \\
& \left( B \right)\dfrac{5}{12} \\
& \left( C \right)\dfrac{5}{24} \\
& \left( D \right)\dfrac{11}{24} \\
\end{align}$

Answer
541.5k+ views
Hint: At first, we need to break down the given shaded area into simpler areas which are easier to find out from $Fig1$ and $Fig2$ . We then add and subtract these fundamental areas from one another to find out the shaded area of $Fig3$ . As we can see, these fundamental areas are one out of the three areas in $Fig1$ and its half, and one out of the four areas in $Fig2$ and its half.
Complete step by step answer:
The shaded area can be shown as the sum of some basic areas which can be simply evaluated. These basic areas are
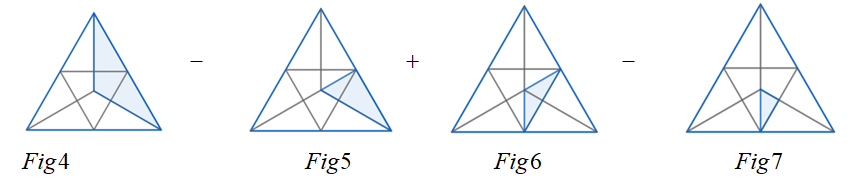
We are given the question that in $Fig1$ , the triangle is divided into three equal parts. The shaded area in $Fig4$ is nothing but one of the individual three areas in $Fig1$ . Thus, if we assume the total area of the triangle to be $A$ , then this shaded area will be one third of the total area, that is $\dfrac{A}{3}$ .
In the shaded part in $Fig3$ , we can clearly see that the shaded area in $Fig4$ has not been entirely taken. Therefore, we need to take away one half of the shaded area in $Fig4$ . This area which needs to be taken away is half that of the shaded area in $Fig4$ which is $\dfrac{1}{2}\times \dfrac{A}{3}=\dfrac{A}{6}$ .
After the above two operations, we see that the shaded area in $Fig3$ has still not been reached. So, we now add the shaded area of $Fig6$ . In $Fig2$ , we have been told that the triangle has been divided equally into four equal areas. Again, if we observe closely, we can see that the shaded area in $Fig6$ is one third of the individual triangle of $Fig2$ . So, we can say that the shaded area of $Fig6$ is $\dfrac{1}{3}\times \dfrac{A}{4}=\dfrac{A}{12}$ .
Again, we need to subtract half the area added previously as more than required had been taken. Half of the previous area means $\dfrac{1}{2}\times \dfrac{A}{12}=\dfrac{A}{24}$ .
After all these operations, we can see that the final area is equal to the area which was required to be found out. This area is equal to $\dfrac{A}{3}-\dfrac{A}{6}+\dfrac{A}{12}-\dfrac{A}{24}=\dfrac{A}{6}+\dfrac{A}{24}=\dfrac{5A}{24}$ . If we want to find out what fraction of area is the shaded one out of the whole triangle, then we need to divide them, which is $\dfrac{\dfrac{5A}{24}}{A}=\dfrac{5}{24}$ .
Therefore, we can conclude that the shaded area in $Fig3$ is $\dfrac{5}{24}$ of the triangle.
Note: In these types of problems, we need to be careful while breaking down the area into fundamental areas and should remember which one to add and which one to subtract. If we get confused, we should name the polygons and then carry out the operations.
Complete step by step answer:
The shaded area can be shown as the sum of some basic areas which can be simply evaluated. These basic areas are

We are given the question that in $Fig1$ , the triangle is divided into three equal parts. The shaded area in $Fig4$ is nothing but one of the individual three areas in $Fig1$ . Thus, if we assume the total area of the triangle to be $A$ , then this shaded area will be one third of the total area, that is $\dfrac{A}{3}$ .
In the shaded part in $Fig3$ , we can clearly see that the shaded area in $Fig4$ has not been entirely taken. Therefore, we need to take away one half of the shaded area in $Fig4$ . This area which needs to be taken away is half that of the shaded area in $Fig4$ which is $\dfrac{1}{2}\times \dfrac{A}{3}=\dfrac{A}{6}$ .
After the above two operations, we see that the shaded area in $Fig3$ has still not been reached. So, we now add the shaded area of $Fig6$ . In $Fig2$ , we have been told that the triangle has been divided equally into four equal areas. Again, if we observe closely, we can see that the shaded area in $Fig6$ is one third of the individual triangle of $Fig2$ . So, we can say that the shaded area of $Fig6$ is $\dfrac{1}{3}\times \dfrac{A}{4}=\dfrac{A}{12}$ .
Again, we need to subtract half the area added previously as more than required had been taken. Half of the previous area means $\dfrac{1}{2}\times \dfrac{A}{12}=\dfrac{A}{24}$ .
After all these operations, we can see that the final area is equal to the area which was required to be found out. This area is equal to $\dfrac{A}{3}-\dfrac{A}{6}+\dfrac{A}{12}-\dfrac{A}{24}=\dfrac{A}{6}+\dfrac{A}{24}=\dfrac{5A}{24}$ . If we want to find out what fraction of area is the shaded one out of the whole triangle, then we need to divide them, which is $\dfrac{\dfrac{5A}{24}}{A}=\dfrac{5}{24}$ .
Therefore, we can conclude that the shaded area in $Fig3$ is $\dfrac{5}{24}$ of the triangle.
Note: In these types of problems, we need to be careful while breaking down the area into fundamental areas and should remember which one to add and which one to subtract. If we get confused, we should name the polygons and then carry out the operations.
Recently Updated Pages
Two men on either side of the cliff 90m height observe class 10 maths CBSE

What happens to glucose which enters nephron along class 10 biology CBSE

Cutting of the Chinese melon means A The business and class 10 social science CBSE

Write a dialogue with at least ten utterances between class 10 english CBSE

Show an aquatic food chain using the following organisms class 10 biology CBSE

A circle is inscribed in an equilateral triangle and class 10 maths CBSE

Trending doubts
The shortest day of the year in India

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the missing number in the sequence 259142027 class 10 maths CBSE




