Question

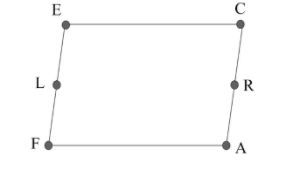
FACE is a parallelogram. L and R are the mid points of EF and AC respectively. Prove that the line segment ER, AL trisect the diagonal FC.

Answer 1

Hint:
In order to show that the line segment \[ER, AL\] trisect \[FC\], first join the points \[E\& L \text{ and } L\& A\]. And join the diagonal \[FC\]. Then use the property of parallelogram in order to prove \[ELAR\] is a parallelogram.

Complete step by step solution:
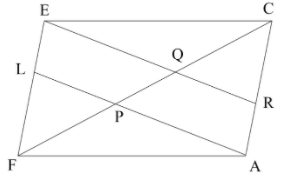
In this question, first we will modify the given diagram as given below,

As given L and R are the midpoint of EF and AC.
So the length of EL and AR is half of the length of EF and AC. The length of EL and AR is given below.
\[
  EL = \dfrac{1}{2}EF \\
  AR = \dfrac{1}{2}AC \\
 \]
As it is given that FACE is a parallelogram. So opposite sides are parallel and equal.
Therefore \[FA = CE {\text{ and }}EL\parallel CE\]. And \[FE = CE {\text{ and }} FE\parallel AC\].
As the length of the line segment EF and AC, so it means \[EF = AC\].
So the half of the EF and AC are also equal, it is shown below.
\[\dfrac{1}{2}EF = \dfrac{1}{2}AC\].
Using the above expression for half of the EF and AC we get the following expression as given below.
\[EL = AR\].
And \[EL\parallel AR\], means EL and AR are parallel.
Thus by using the property of the parallelogram, ELAR is also a parallelogram.
So \[ER\parallel LA {\text{and }}EQ\parallel LP\]
In the triangle \[APC\] we have \[R\] is the midpoint of \[AC\], and \[P\] is the midpoint of \[FQ\].
So, the length of the line segment \[FP \& PQ\] are equal; it means \[FP = PQ \left( 1 \right)\].
In the triangle \[PFE\] we have \[L\] is the midpoint of \[FE\].
Also, as \[Q\] is the midpoint of \[CP\].
So we get the length of the line segments \[CQ \& PQ\] are equal, it means \[CQ = PQ \left( 2 \right)\]
Using the above expression (1) and (2) we find that the length of the line segments\[FP,PQ\& QC\] are equal; it means \[FP = PQ = QC\].

Hence the above proof is showing that \[ER,AL\] trisect \[FC\].

Note:
We know that in a parallelogram the opposite sides are parallel and equal. In order to prove a quadrilateral is a parallelogram it is enough to prove that one pair of opposite sides are parallel and equal.