Question

Explain why $ 15 \times 7 + 7 $ is a composite number.

Answer 1

Hint: A composite number is a positive integer that can be formed by multiplying two smaller positive integers. That integers has at least one divisor other than $ 1 $ and itself.


Complete step by step solution::
The given number is: $ 15 \times 7 + 7 $
There are two terms in the given number and $ 7 $is a common factor.
We take $ 7 $as common, then we have
$ 15 \times 7 + 7 = 7\left( {15 \times 1 + 1} \right) $
$ 15 \times 7 + 7 = 7\left( {15 + 1} \right) $
$ 15 \times 7 + 7 = 7\left( {16} \right) $
$ 15 \times 7 + 7 = 112 $
When we factorize\[112\], we will get

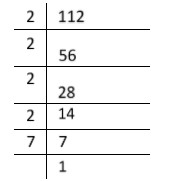
$ 112 = 2 \times 2 \times 2 \times 2 \times 7 $
$ 112 = {2^4} \times 7 $
This number is divisible by $ 2,4,7,8 $and $ 16 $, which means that it has more than two factors.
Therefore, $ 15 \times 7 + 7 $ is a composite number
Additional information: the divisibility rule is given below:
(i) Divisibility rule of $ 2 $: Which states that for a number to be divisible by $ 2 $, the unit digit must have \[0,2,4,6\]or \[8\] in units place.
(ii) Divisibility rule of $ 4 $: Which states that for a number to be divisible by $ 4 $, the unit and tens digit should be divisible by $ 4 $
(iii) Divisibility rule of $ 7 $: We need to double the last digit of the number and then subtract it from the remaining number. If the result is divisible by $ 7 $, then the original number will also be divisible by $ 7 $.

Note: Different types of numbers are:
(i) Natural number: \[1,2,3,4,\]------
(ii) Whole number:\[\;0,1,2,3,4,\] ------
(iii) Integers: \[ - 4, - 3, - 2, - 1,0,1,2,3,4,\]-----
(iv) Positive integers: \[1,2,3,\]-----
(v) Negative integers: \[ - 4, - 3, - 2, - 1\]