Question

Draw the circles whose equation are \[3{x^2} + 3{y^2} = 4x\]

Answer 1

Hint: We can convert the given equation to its standard form ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}$, to get the radius and center. Then we can draw the circle with the help of the radius and the center.

Complete step by step answer:

We have equation of the circle as $3{x^2} + 3{y^2} = 4x$
Dividing throughout with 3, we get,
\[{x^2} + {y^2} - \dfrac{4}{3}x = 0\]
We can factories the x term.
${x^2} + {y^2} - 2 \times \dfrac{2}{3} \times x = 0$
Adding ${\left( {\dfrac{2}{3}} \right)^2}$on both sides, we get,
${x^2} + {y^2} - 2 \times \dfrac{2}{3} \times x + {\left( {\dfrac{2}{3}} \right)^2} = {\left( {\dfrac{2}{3}} \right)^2}$
Using the identity ${\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}$, we get,
\[{\left( {x - \dfrac{2}{3}} \right)^2} + {y^2} = {\left( {\dfrac{2}{3}} \right)^2}\]
Now we can compare this equation with the standard equation of a circle, ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}$, we get, radius as $r = \dfrac{2}{3}$ and center $\left( {\dfrac{2}{3},0} \right)$
Now we can draw the circle.

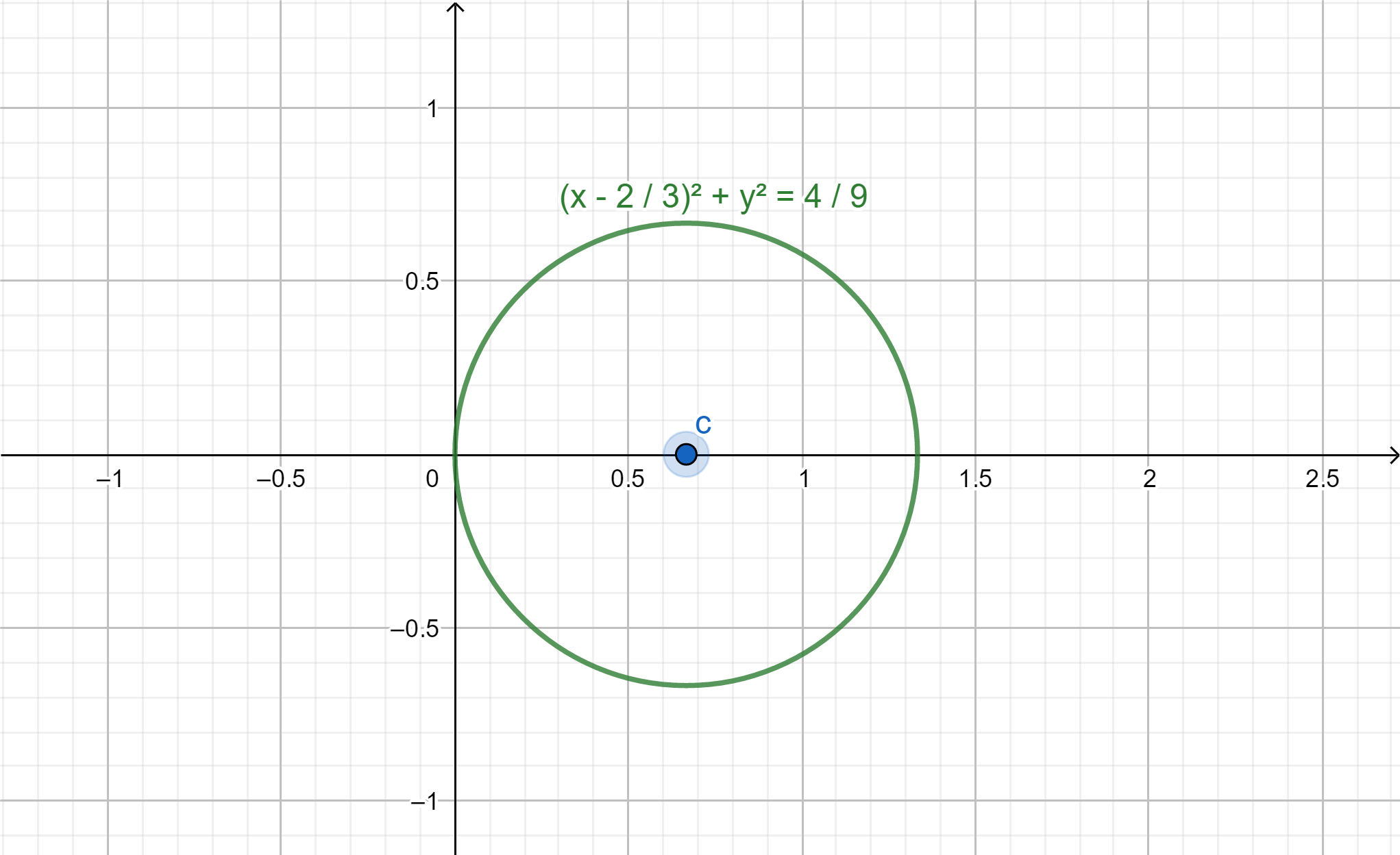
Note: The standard equation of a circle with radius r and center $\left( {a,b} \right)$is given by, ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}$. Any equation of a circle can be changed to its standard form by applying some algebra. From the standard equation we can find the center and the radius of the circle. On a graph we can verify our circle by taking a point on the circle and substitute in the equation of circle. If the point satisfies the equation, our circle is correct.

Additional information:A circle is defined as the collection of all points that are equidistant from a given point. This point from which all points are equidistant is known as the center of the circle. The distance from the center to the points is known as the radius of the circle. If a point lies on the circle, it satisfies the circle’s equation.