Question

Draw any angle with vertex O. Take a point A on one of its arms and B on another such that OA = OB. Draw the perpendicular bisectors of \[\overline{OA\text{ }}\text{ and }\overline{OB}\]. Let them meet at P. Is PA = PB?

Answer 1

Hint: In this question, we will perform some basic geometric construction. We will draw an angle with vertex O, then we will draw a perpendicular bisector on both the arms of the angle, which will intersect at P. In the last step we will join AP and BP and measure the length of AP and BP using a divider.

Complete step-by-step solution:
It is given in the question that we have to draw any angle with vertex O. Take a point A on one of its arms and B on another such that OA = OB. Draw the perpendicular bisectors of \[\overline{OA\text{ }}\text{ and }\overline{OB}\]. Let them meet at P. And we have been asked to find whether PA = PB.
For constructing the angles and the perpendicular bisectors we need the following materials.
Pencils, compass, divider, eraser, and ruler.
So, we will first draw an angle with the vertex O. So, we get,

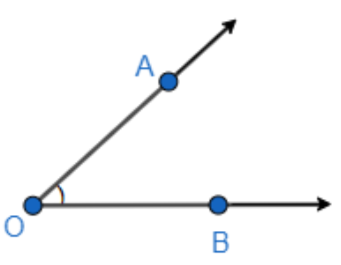
Here, we have A and B as the points on the arms of the angle $\angle AOB$, also the length of OA is equal to the length of OB as it is mentioned in the question. So, we can write,
OA = OB
Now, we will draw perpendicular bisectors of OA and OB respectively.
We will draw the perpendicular bisector of OA first.
So, for drawing the perpendicular bisector of OA, we will follow the following steps.
Step 1: We will first cut an arc assuming O as the center having the radius more than half of OA, and then again we will draw an arc from point A, such that it cuts the previously drawn arc. While drawing the arcs, we will draw it above and below the arm which has the point A. So, the construction will look as follows.

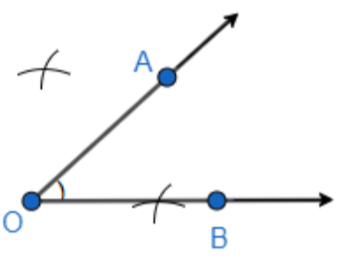
Step 2: We will join the two arcs such that it will perpendicularly bisect OA. So, we get.

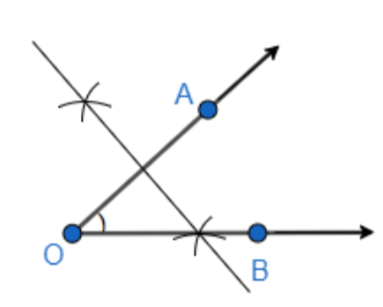
Now, we will again repeat these two steps for, drawing the perpendicular bisector of OB.
Step 1: We will first cut an arc assuming O as the center having the radius more than half of OB, and then again we will draw an arc from point A, such that it cuts the previously drawn arc. While drawing the arcs, we will draw it above and below the arm which has the point B. So, the construction will look as follows.

Step 2: We will join the two arcs such that it will perpendicularly bisect OB. So, we get.

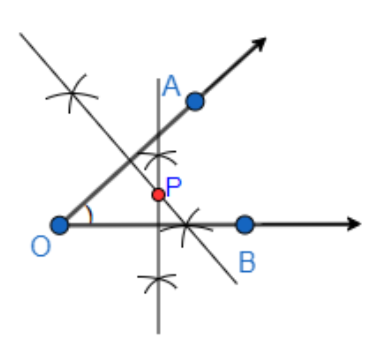
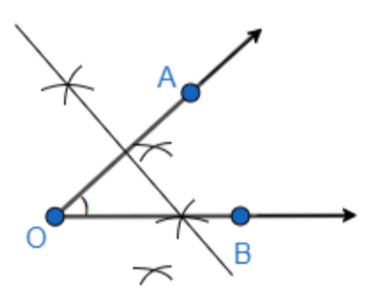
We have named the intersection point of the perpendicular bisectors as point P.
Now, we will join the points A and P, and also the points B and P. So, we get,

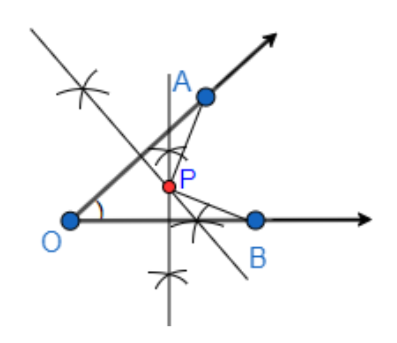
Now, we will compare AP with BP, using the divider.
So, for comparing AP and BP, we will first place one of the ends of the divider on point A, and then we will extend it till point P and place the other end of the divider on point P. This gives us the distance AP on the divider.
Next, we will place one of the ends of the same divider with the distance AP on it, on the point B, and then we will see if the other end of the divider touches the point P exactly.
So, here, we will be able to observe that the other end of the divider meets at point P. So, from this, we can conclude that the distance AP and BP are the same.
Therefore, we get, PA = PB. Hence, it is true and verified.

Note: In order to get the correct and accurate results, the students must make sure that they have followed all the construction steps correctly. Also, the students must understand the terms angle, vertex, and arms, only then they will be able to complete the question. So, an angle is formed when the two rays intersect at a point. The vertex of an angle is the common endpoint where the two rays meet. And, arms of an angle are the rays which intersect to form an angle.