Question

Draw \[\angle PQR\] of measure\[{75^ \circ }\] and find its line of symmetry.

Answer 1

Hint:: Geometry is the branch of mathematics which studies about the size, shapes, position angles and dimension.


Complete step by step solution:
The angle which is to be drawn is in between the two lines hence, we have to draw a straight line QR which will be the base for the angle.
Now using a compass adjust compass to a length and draw an arc with Q being the Centre cutting the line segment QR at P,

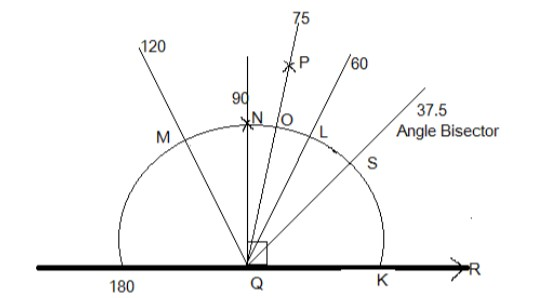
With the same length of compass make a mark on the arc starting from the line QR at K and name the mark as L which will be equal to \[{60^ \circ }\] and make a another cut from L with the same length at M making an angle of \[{120^ \circ }\].
Now using the compass measure the distance between the mark L and M then bisect L and M at N using the same length by compass keeping L and M as base then join a line from N to Q which will make an angle of \[{90^ \circ }\].
Now we measure the length between L and N and bisect the point at O which will be equal to \[{75^ \circ }\].
Hence we get the angle\[{75^ \circ }\] at O.
Now we have to draw a line of symmetry which will be equal to is \[\dfrac{{{{75}^ \circ }}}{2} = {37.5^ \circ }\], by bisecting the points O and K using the compass.

Note: It is to be noted down here that the angle bisector is the priority thing which is to be kept in mind while plotting the angle. Always the angle could be plotted by using the concept of angle bisectors.