Question

Draw a circle with center \[C\] and radius 3.4 cm. Draw any chord \[\overline {AB} \]. Construct the perpendicular bisector of \[\overline {AB} \] and examine if it passes through \[C\].

Answer 1

Hint: In this question, first of all, taken a point C and draw a circle of radius 3.4 cm using a ruler and compass with center C. Then make a chord anywhere in the circle and name the chord as AB. Further, make perpendicular bisector of chord AB by taking a length of more than half of the radius. Observe whether the drawn perpendicular bisector is passing through the center of the circle or not. So, use this concept to reach the solution to the given problem.

Complete step-by-step solution:
Follow the below steps to construct the required circle with chord AB and its perpendicular bisector:
Construction:
1. Mark a point \[C\] as the center of the circle

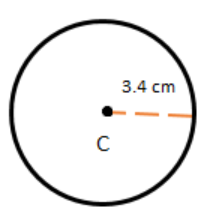
2. The given radius of the circle is 3.4 cm. Now, take 3.4 cm by using a ruler and compass. Then keeping the compass opened the same length, we keep the pointed end at the center, and draw a circle using the pencil end of the compass.

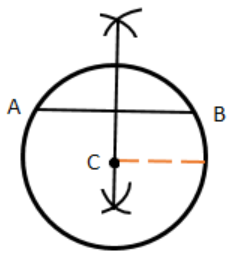
3. Then draw a chord \[\overline {AB} \] anywhere in the circle.

4. Now, we have to draw a perpendicular bisector of AB. With A as center, and radius more than half AB, draw an arc on the bottom of AB. With B as a centre and the same radius as before, draw an arc on top and bottom of AB. Join both the points obtained.

5. Let the two arcs intersect above AB is point X and where the two arcs intersect below AB is point XY. We note that here perpendicular bisector of AB passes through point C.

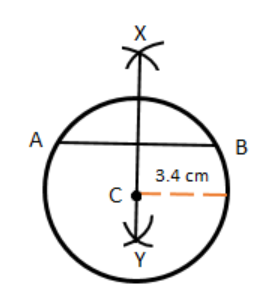
So, the perpendicular to the chord passes through the center C of the circle.

Note: A perpendicular bisector of a line segment is a line segment perpendicular to and passing through the midpoint of the line segment. Always remember that the perpendicular bisector of any chord in the circle passes through the center of the circle.