Question

Donna’s TV screen is $20$ inches long. If the diagonal measures $25$ inches, How long is the width of Donna’s TV?

Answer 1

Hint: Here in the problem is a basic right angled triangle. So we have to use the Pythagoras Theorem for determining the remaining or required length of a side. The right angled triangle has three sides. Consider $'a','b','c'$ as their sides. Then apply the theorem and find the required side of the following.

Complete step by step solution:
Here, we have
Donna’s TV screen is $20$ inches long.
If the diagonal measures $25$ inches long.
So,
We have to determine the width of Donna’s TV. This problem is a basic right triangle issue, therefore we have to apply Pythagora's theorem. For determining the missing length of the slide.

The Pythagoras theorem states that the square of hypotenuse (diagonal) of any right triangle is equal to the square of two legs.
So,
Here we have ${{a}^{2}}+{{b}^{2}}={{c}^{2}}$
For this type of situation the television screen is cut by a diagonal of $25$ inches and length of its side is $20$ inches.

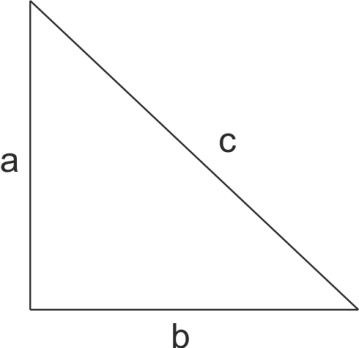
Now, we can use ${{a}^{2}}+{{b}^{2}}={{c}^{2}}$ for determine the missing side.
Where, $a=20,b=?,c=25$
${{a}^{2}}+{{b}^{2}}={{c}^{2}}$
$\Rightarrow {{\left( 20 \right)}^{2}}+{{\left( n \right)}^{2}}={{\left( 25 \right)}^{2}}$
$\Rightarrow 400+{{\left( n \right)}^{2}}=625$
$\Rightarrow{{n}^{2}}=625-400$
$\Rightarrow{{n}^{2}}=225$
$\therefore n=\sqrt{225}$
$\therefore n=15$

Hence, donna’s TV has a width of $15$ inches.

Additional Information:
The Pythagoras theorem can be used on any triangle to tell us whether or not it is a right triangle or it also relates between the slides of the right angle triangle. Pythagora's theorem is basically used to find the length of an unknown side and angle of a triangle by this theorem we will derive base, perpendicular and hypotenuse formula. In this Pythagoras theorem which states that in a right angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides. We can also name it as perpendicular. Base and hypotenuse. So, the longest side is the hypotenuse as it is opposite to angle$90{}^\circ $. The sides of a triangle have positive integer value, when they are square put into an equation. The formula for this theorem is (Hypotenuse ${{)}^{2}}=$(Perpendicular) $+$ (Base${{)}^{2}}$ or ${{c}^{2}}={{a}^{2}}+{{b}^{2}}$

Note: The Pythagoras theorem is only applicable at right angled triangles. You have to remember that in formula squaring a number means to multiply it by itself. We can say that if the sum is equal to its square of hypotenuse then it is right angles triangle, If two sides are not equal to its square of hypotenuse then it is right angle triangle, If two sides are not equal then the triangle is not right angled triangle for finding this all you have to ensure that you have the measurement of all three sides of triangle. So, remember these key points for solving this type of question.