Question

Do the sides, \[15,17\] and \[8\] form a right triangle? If so, which side is the hypotenuse?
A. \[15\]
B. \[17\]
C. \[8\]
D. \[10\]

Answer 1

Hint: We are asked whether the triangle formed by the given sides form a right angled triangle. First recall the Pythagoras theorem and its condition for which a triangle can be called a right angled triangle. Check whether the sides given satisfy those conditions.

Complete step-by-step answer:
Given, the sides are \[15,17\] and \[8\]
Let the given sides be of a triangle ABC where
 \[{\text{AB}} = 15\]
 \[{\text{AC}} = 17\]
 \[{\text{BC}} = 8\]
For a triangle to be right angled triangle, it must satisfy Pythagoras theorem which says
 \[{\text{hypotenus}}{{\text{e}}^2} = {\text{bas}}{{\text{e}}^2} + {\text{perpendicula}}{{\text{r}}^2}\]
And hypotenuse is always the longest side.
Let us draw the triangle ABC

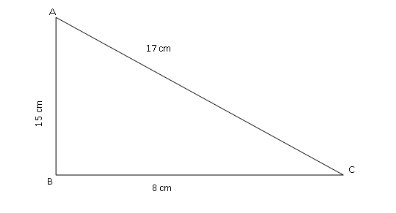
Here the longest side is \[{\text{AC}} = 17\] , so for ABC to be a right angled triangle we must have
 \[{\text{A}}{{\text{C}}^2} = {\text{A}}{{\text{B}}^2} + {\text{B}}{{\text{C}}^2}\]
Let us calculate L.H.S and R.H.S separately,
L.H.S \[ = {\text{A}}{{\text{C}}^2} = {17^2} = 289\]
R.H.S \[ = {\text{A}}{{\text{B}}^2} + {\text{B}}{{\text{C}}^2}\]
 \[
   = {15^2} + {8^2} \\
   = 225 + 64 \\
   = 289
\]
We observe that L.H.S \[ = \] R.H.S
Therefore, triangle ABC or the given triangle is a right angled triangle and its hypotenuse is \[17\] .
So, the correct answer is “Option B”.

Note: Always remember the condition given by Pythagoras theorem as it is used in most of the problems. Hypotenuse is always the longest side and it is to the opposite of the right angle of the triangle. Pythagora's theorem is also used in our day to day life such as for calculating steepness of hill or mountain, height of a building, length of a ladder, used in construction and architecture works and used to find the shortest distance between two given points and also for many other purposes.