Question

What is the distance of the point (p,q,r) from the x-axis?

Answer 1

Hint: In this question, we need to find the distance of the point (p,q,r) from the x axis. For this, we will evaluate the point on the x axis which is perpendicular to (p,q,r) and then find the distance between two points obtained. Distance between two points $\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ is given by \[\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}\].

Complete step-by-step solution
Here, we need to find the distance of the point (p,q,r) from the x-axis. Our diagram looks like this,

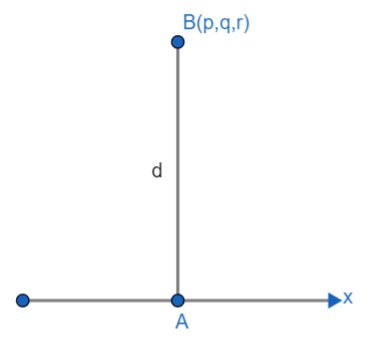
Let us suppose B as point (p,q,r) and let us suppose the point A on the x-axis is perpendicular from (p,q,r). As we know, a point on the x-axis does not have any value of y coordinate and z coordinate. Hence, any point A on the x-axis will have y coordinate and z coordinate as o. Since A is perpendicular to (p,q,r) so x coordinate will be p only. Hence point A will be (p,0,0). So, now we need to find the distance between B(p,q,r) and A(p,0,0).
As we know, distance between two points $\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ is given by \[d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}\].
So here ${{x}_{1}}$ is equal to p, ${{x}_{2}}$ is equal to p, ${{y}_{1}}$ is equal to q, ${{y}_{2}}$ is equal to 0, ${{z}_{1}}$ is equal to r and ${{z}_{2}}$ is equal to 0.
Hence, distance between B(p,q,r) and A(p,0,0) becomes,
\[\begin{align}
  & \Rightarrow d=\sqrt{{{\left( p-p \right)}^{2}}+{{\left( q-0 \right)}^{2}}+{{\left( r-0 \right)}^{2}}} \\
 & \Rightarrow d=\sqrt{0+{{q}^{2}}+{{r}^{2}}} \\
 & \Rightarrow d=\sqrt{{{q}^{2}}+{{r}^{2}}} \\
\end{align}\]
Hence, the distance between point (p,q,r) and x axis is $\sqrt{{{q}^{2}}+{{r}^{2}}}$.

Note: Students should carefully find the coordinates of the point on the x-axis from which distance will be measured. Remember that, distance from any point to a line or plane is equal to the distance between the point and the foot of the perpendicular on the plane (or line). Students should note that we can take ${{y}_{1}}$ as 0 and ${{y}_{2}}$ as q also. Similarly, ${{z}_{1}}$ as 0 and ${{z}_{2}}$ as “r” also. It will result in the same because terms will be squared and we know that the distance from A to B is equal to the distance from B to A.