$\Delta ABC$ is right angled at C. If $A=\left( 1,2 \right)$ , and the circumcenter of $\Delta ABC$ is at $\left( 6,2 \right)$ and length of side AC is 8 units, then find the possible coordinates of C .
Answer
Verified639.9k+ views
Hint: First, we will assume a right angled at C then we will use the midpoint formula that is $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$ to find the coordinate of B since we know that the circumcenter lies at the midpoint of the hypotenuse and then we will find the length of AB and BC using the distance formula: \[d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\] then we will apply the Pythagoras theorem : ${{\left( \text{Hypotenuse} \right)}^{2}}={{\left( \text{Base} \right)}^{2}}+{{\left( \text{Perpendicular} \right)}^{2}}$and get two equations in the unknown coordinates of C and then we will solve them to get the answer.
Complete step-by-step solution
Now, it is given that the $\Delta ABC$ is right-angled at C, therefore it will look like the following figure:
Here, AB is the hypotenuse, BC is the base and AC is the perpendicular.
Now, if we have two points say $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ then according to the midpoint formula we know that the coordinates of midpoint say \[\left( {{x}_{m}},{{y}_{m}} \right)\] then: ${{x}_{m}}=\dfrac{{{x}_{1}}+{{x}_{2}}}{2},{{y}_{m}}=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}\Rightarrow \left( {{x}_{m}},{{y}_{m}} \right)=\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
Now, it is given that $A=\left( 1,2 \right)$ and the circumcenter let’s say P has the coordinates: $\left( 6,2 \right)$. Let’s say $B=\left( {{b}_{1}},{{b}_{2}} \right)$
Now, we know that the circumcenter lies at the midpoint of the hypotenuse side of a right-angled triangle therefore P will be the midpoint of AB.
Now, we will apply the midpoint formula , therefore: $\left( 6,2 \right)=\left( \dfrac{1+{{b}_{1}}}{2},\dfrac{2+{{b}_{2}}}{2} \right)$
$\Rightarrow 6=\dfrac{1+{{b}_{1}}}{2},2=\dfrac{2+{{b}_{2}}}{2}\Rightarrow {{b}_{1}}=11,{{b}_{2}}=2$
Therefore: $B=\left( 11,2 \right)$ .
Now, we have: $A=\left( 1,2 \right),B=\left( 11,2 \right)$ and let’s say $C=\left( {{c}_{1}},{{c}_{2}} \right)$
Now, we know that according to the distance formula, the distance between$\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is as follows: \[d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
Now, it is given that then the length of AC is 8 units,
Now we will apply the distance formula on $A=\left( 1,2 \right)$ and $C=\left( {{c}_{1}},{{c}_{2}} \right)$ , therefore: $8=\sqrt{{{\left( 1-{{c}_{1}} \right)}^{2}}+{{\left( 2- {{c}_{2}} \right)}^{2}}}$ ,
Now, we will square both the sides: $64={{\left( 1-{{c}_{1}} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}}\text{ }........\left( 1 \right)$
Now, we will find the length of AB by applying the distance formula on $A=\left( 1,2 \right)$ and $B=\left( 11,2 \right)$ :
$AB=\sqrt{{{\left( 11-1 \right)}^{2}}+{{\left( 2-2 \right)}^{2}}}=\sqrt{{{\left( 10 \right)}^{2}}}=10$
Therefore, AB is 10 units.
Similarly, we will apply the distance formula between B and C to find the length of BC, we have: $B=\left( 11,2 \right)$ and $C=\left( {{c}_{1}},{{c}_{2}} \right)$ :
$BC=\sqrt{{{\left( 11-{{c}_{1}} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}}}$
Now, we will square both the sides: $B{{C}^{2}}={{\left( 11-{{c}_{1}} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}}\text{ }........\left( 2 \right)$
Now, we will apply the Pythagoras theorem that is: ${{\left( \text{Hypotenuse} \right)}^{2}}={{\left( \text{Base} \right)}^{2}}+{{\left( \text{Perpendicular} \right)}^{2}}$
Now, we will apply it on the given triangle and here AB is the hypotenuse, BC is the base and AC is the perpendicular. Therefore: $A{{B}^{2}}=B{{C}^{2}}+A{{C}^{2}}$
Now, we know that AC is 8 units , AB is 10 units and we will put the value of BC from equation 2 and then we will get:
$\begin{align}
& \Rightarrow {{\left( 10 \right)}^{2}}={{\left( 11-{{c}_{1}} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}}+{{\left( 8 \right)}^{2}} \\
& \Rightarrow 100={{\left( 11-{{c}_{1}} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}}+64 \\
& \Rightarrow 36={{\left( 11-{{c}_{1}} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}}\text{ }.........\left( 3 \right) \\
\end{align}$
We will subtract equation 3 from equation 1 and therefore we will get:
$\begin{align}
& \Rightarrow 64-36=\left[ {{\left( 1-{{c}_{1}} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}} \right]-\left[ {{\left( 11-{{c}_{1}} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}} \right] \\
& \Rightarrow 28={{\left( 1-{{c}_{1}} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}}-{{\left( 11-{{c}_{1}} \right)}^{2}}-{{\left( 2-{{c}_{2}} \right)}^{2}} \\
& \Rightarrow 28={{\left( 1-{{c}_{1}} \right)}^{2}}-{{\left( 11-{{c}_{1}} \right)}^{2}} \\
\end{align}$
Now, we will apply the identity ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$ on the right hand side.
\[\begin{align}
& \Rightarrow 28={{\left( 1-{{c}_{1}} \right)}^{2}}-{{\left( 11-{{c}_{1}} \right)}^{2}} \\
& \Rightarrow 28=\left( {{1}^{2}}+c_{1}^{2}-2{{c}_{1}} \right)-\left( {{11}^{2}}+c_{1}^{2}-22{{c}_{1}} \right) \\
& \Rightarrow 28=1+c_{1}^{2}-2{{c}_{1}}-121-c_{1}^{2}+22{{c}_{1}} \\
& \Rightarrow 28=20{{c}_{1}}-120 \\
\end{align}\]
We will now simplify the equation to find the value of ${{c}_{1}}$:
$\begin{align}
& \Rightarrow 28=20{{c}_{1}}-120\Rightarrow 148=20{{c}_{1}} \\
& \Rightarrow \dfrac{148}{20}={{c}_{1}} \\
& \Rightarrow {{c}_{1}}=\dfrac{37}{5} \\
\end{align}$
Now, we will put this value of ${{c}_{1}}$ in equation 1 that is $64={{\left( 1-{{c}_{1}} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}}$ :
$\begin{align}
& \Rightarrow 64={{\left( 1-\dfrac{37}{5} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}}\Rightarrow 64={{\left( \dfrac{5-37}{5} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}} \\
& \Rightarrow 64={{\left( \dfrac{-32}{5} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}}\Rightarrow 64=\dfrac{1024}{25}+{{\left( 2-{{c}_{2}} \right)}^{2}} \\
& \Rightarrow 64-\dfrac{1024}{25}={{\left( 2-{{c}_{2}} \right)}^{2}}\Rightarrow \dfrac{1600-1024}{25}={{\left( 2-{{c}_{2}} \right)}^{2}} \\
& \Rightarrow \dfrac{576}{25}={{\left( 2-{{c}_{2}} \right)}^{2}} \\
\end{align}$
Now, we will take square roots on both the sides: $\Rightarrow \sqrt{\dfrac{576}{25}}=\pm \left( 2-{{c}_{2}} \right)\Rightarrow \dfrac{24}{5}=\pm \left( 2-{{c}_{2}} \right)$
Now, we will ignore the negative value as with the negative value triangle will not get formed, therefore:
$\begin{align}
& \Rightarrow \dfrac{24}{5}=2-{{c}_{2}}\Rightarrow {{c}_{2}}=2-\dfrac{24}{5} \\
& \Rightarrow {{c}_{2}}=\dfrac{10-24}{5} \\
& \Rightarrow {{c}_{2}}=\dfrac{-14}{5} \\
\end{align}$
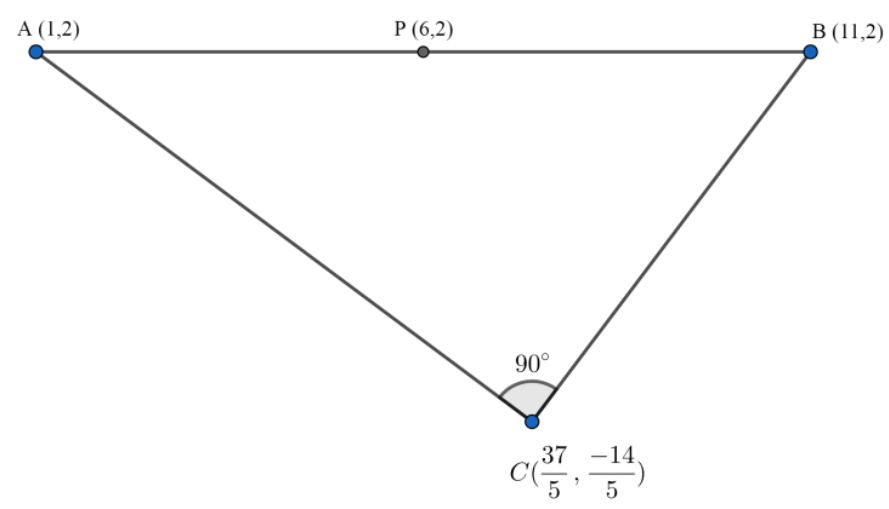
Hence, the coordinates of $C=\left( \dfrac{37}{5},\dfrac{-14}{5} \right)$
And the triangle will look like the following figure:
Note: We must be careful while applying the formula that is the midpoint formula, distance formula, and the Pythagoras theorem as there are calculations involved and even if we make a small mistake the whole answer will be wrong. For example, while applying Pythagoras theorem on the triangle ABC, if we write: $A{{C}^{2}}=B{{C}^{2}}+A{{B}^{2}}$ instead of $A{{B}^{2}}=B{{C}^{2}}+A{{C}^{2}}$ then we will get a negative value of BC which is not valid as the length should be positive in order to form a triangle. And always mention the general formula first and then apply it.
Complete step-by-step solution
Now, it is given that the $\Delta ABC$ is right-angled at C, therefore it will look like the following figure:
Here, AB is the hypotenuse, BC is the base and AC is the perpendicular.
Now, if we have two points say $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ then according to the midpoint formula we know that the coordinates of midpoint say \[\left( {{x}_{m}},{{y}_{m}} \right)\] then: ${{x}_{m}}=\dfrac{{{x}_{1}}+{{x}_{2}}}{2},{{y}_{m}}=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}\Rightarrow \left( {{x}_{m}},{{y}_{m}} \right)=\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
Now, it is given that $A=\left( 1,2 \right)$ and the circumcenter let’s say P has the coordinates: $\left( 6,2 \right)$. Let’s say $B=\left( {{b}_{1}},{{b}_{2}} \right)$
Now, we know that the circumcenter lies at the midpoint of the hypotenuse side of a right-angled triangle therefore P will be the midpoint of AB.
Now, we will apply the midpoint formula , therefore: $\left( 6,2 \right)=\left( \dfrac{1+{{b}_{1}}}{2},\dfrac{2+{{b}_{2}}}{2} \right)$
$\Rightarrow 6=\dfrac{1+{{b}_{1}}}{2},2=\dfrac{2+{{b}_{2}}}{2}\Rightarrow {{b}_{1}}=11,{{b}_{2}}=2$
Therefore: $B=\left( 11,2 \right)$ .
Now, we have: $A=\left( 1,2 \right),B=\left( 11,2 \right)$ and let’s say $C=\left( {{c}_{1}},{{c}_{2}} \right)$
Now, we know that according to the distance formula, the distance between$\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is as follows: \[d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
Now, it is given that then the length of AC is 8 units,
Now we will apply the distance formula on $A=\left( 1,2 \right)$ and $C=\left( {{c}_{1}},{{c}_{2}} \right)$ , therefore: $8=\sqrt{{{\left( 1-{{c}_{1}} \right)}^{2}}+{{\left( 2- {{c}_{2}} \right)}^{2}}}$ ,
Now, we will square both the sides: $64={{\left( 1-{{c}_{1}} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}}\text{ }........\left( 1 \right)$
Now, we will find the length of AB by applying the distance formula on $A=\left( 1,2 \right)$ and $B=\left( 11,2 \right)$ :
$AB=\sqrt{{{\left( 11-1 \right)}^{2}}+{{\left( 2-2 \right)}^{2}}}=\sqrt{{{\left( 10 \right)}^{2}}}=10$
Therefore, AB is 10 units.
Similarly, we will apply the distance formula between B and C to find the length of BC, we have: $B=\left( 11,2 \right)$ and $C=\left( {{c}_{1}},{{c}_{2}} \right)$ :
$BC=\sqrt{{{\left( 11-{{c}_{1}} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}}}$
Now, we will square both the sides: $B{{C}^{2}}={{\left( 11-{{c}_{1}} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}}\text{ }........\left( 2 \right)$
Now, we will apply the Pythagoras theorem that is: ${{\left( \text{Hypotenuse} \right)}^{2}}={{\left( \text{Base} \right)}^{2}}+{{\left( \text{Perpendicular} \right)}^{2}}$
Now, we will apply it on the given triangle and here AB is the hypotenuse, BC is the base and AC is the perpendicular. Therefore: $A{{B}^{2}}=B{{C}^{2}}+A{{C}^{2}}$
Now, we know that AC is 8 units , AB is 10 units and we will put the value of BC from equation 2 and then we will get:
$\begin{align}
& \Rightarrow {{\left( 10 \right)}^{2}}={{\left( 11-{{c}_{1}} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}}+{{\left( 8 \right)}^{2}} \\
& \Rightarrow 100={{\left( 11-{{c}_{1}} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}}+64 \\
& \Rightarrow 36={{\left( 11-{{c}_{1}} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}}\text{ }.........\left( 3 \right) \\
\end{align}$
We will subtract equation 3 from equation 1 and therefore we will get:
$\begin{align}
& \Rightarrow 64-36=\left[ {{\left( 1-{{c}_{1}} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}} \right]-\left[ {{\left( 11-{{c}_{1}} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}} \right] \\
& \Rightarrow 28={{\left( 1-{{c}_{1}} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}}-{{\left( 11-{{c}_{1}} \right)}^{2}}-{{\left( 2-{{c}_{2}} \right)}^{2}} \\
& \Rightarrow 28={{\left( 1-{{c}_{1}} \right)}^{2}}-{{\left( 11-{{c}_{1}} \right)}^{2}} \\
\end{align}$
Now, we will apply the identity ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$ on the right hand side.
\[\begin{align}
& \Rightarrow 28={{\left( 1-{{c}_{1}} \right)}^{2}}-{{\left( 11-{{c}_{1}} \right)}^{2}} \\
& \Rightarrow 28=\left( {{1}^{2}}+c_{1}^{2}-2{{c}_{1}} \right)-\left( {{11}^{2}}+c_{1}^{2}-22{{c}_{1}} \right) \\
& \Rightarrow 28=1+c_{1}^{2}-2{{c}_{1}}-121-c_{1}^{2}+22{{c}_{1}} \\
& \Rightarrow 28=20{{c}_{1}}-120 \\
\end{align}\]
We will now simplify the equation to find the value of ${{c}_{1}}$:
$\begin{align}
& \Rightarrow 28=20{{c}_{1}}-120\Rightarrow 148=20{{c}_{1}} \\
& \Rightarrow \dfrac{148}{20}={{c}_{1}} \\
& \Rightarrow {{c}_{1}}=\dfrac{37}{5} \\
\end{align}$
Now, we will put this value of ${{c}_{1}}$ in equation 1 that is $64={{\left( 1-{{c}_{1}} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}}$ :
$\begin{align}
& \Rightarrow 64={{\left( 1-\dfrac{37}{5} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}}\Rightarrow 64={{\left( \dfrac{5-37}{5} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}} \\
& \Rightarrow 64={{\left( \dfrac{-32}{5} \right)}^{2}}+{{\left( 2-{{c}_{2}} \right)}^{2}}\Rightarrow 64=\dfrac{1024}{25}+{{\left( 2-{{c}_{2}} \right)}^{2}} \\
& \Rightarrow 64-\dfrac{1024}{25}={{\left( 2-{{c}_{2}} \right)}^{2}}\Rightarrow \dfrac{1600-1024}{25}={{\left( 2-{{c}_{2}} \right)}^{2}} \\
& \Rightarrow \dfrac{576}{25}={{\left( 2-{{c}_{2}} \right)}^{2}} \\
\end{align}$
Now, we will take square roots on both the sides: $\Rightarrow \sqrt{\dfrac{576}{25}}=\pm \left( 2-{{c}_{2}} \right)\Rightarrow \dfrac{24}{5}=\pm \left( 2-{{c}_{2}} \right)$
Now, we will ignore the negative value as with the negative value triangle will not get formed, therefore:
$\begin{align}
& \Rightarrow \dfrac{24}{5}=2-{{c}_{2}}\Rightarrow {{c}_{2}}=2-\dfrac{24}{5} \\
& \Rightarrow {{c}_{2}}=\dfrac{10-24}{5} \\
& \Rightarrow {{c}_{2}}=\dfrac{-14}{5} \\
\end{align}$
Hence, the coordinates of $C=\left( \dfrac{37}{5},\dfrac{-14}{5} \right)$
And the triangle will look like the following figure:
Note: We must be careful while applying the formula that is the midpoint formula, distance formula, and the Pythagoras theorem as there are calculations involved and even if we make a small mistake the whole answer will be wrong. For example, while applying Pythagoras theorem on the triangle ABC, if we write: $A{{C}^{2}}=B{{C}^{2}}+A{{B}^{2}}$ instead of $A{{B}^{2}}=B{{C}^{2}}+A{{C}^{2}}$ then we will get a negative value of BC which is not valid as the length should be positive in order to form a triangle. And always mention the general formula first and then apply it.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success
State BPT theorem and prove it class 10 maths CBSE
A peacock is sitting on the top of a pillar which -class-10-maths-CBSE
Railways Women Helpline Number?
Explain the refraction of light through a glassslab class 10 physics CBSE
a Why did Mendel choose pea plants for his experiments class 10 biology CBSE
Trending doubts
Explain the Treaty of Vienna of 1815 class 10 social science CBSE
10 examples of evaporation in daily life with explanations
What is the full form of POSCO class 10 social science CBSE
Five things I will do to build a great India class 10 english CBSE
Write short note on buckyball class 10 chemistry CBSE
Make a sketch of the human nerve cell What function class 10 biology CBSE