Question

Define Center of mass of a system of particles. Find center of mass of three particles at the vertices of an equilateral triangle. The masses of the particle are $100\,gm,\,150\,gm$ and $200\,gm$ . Each side of the equilateral triangle is 0.5 m long. [Take $100\,gm$ at origin]

Answer 1

Hint:To solve this question, first you need to know and define the center of mass of a system of particles. Then, you’ll need to draw an equilateral triangle and put the particles on each vertex and first, find X-coordinate of Center of mass and Y-coordinate of center of mass to finally reach the answer to the numerical part of the question.

Complete step by step answer:
The center of mass is referred to as a position which is relative to an object or system of objects and is the average position of all the parts of the system, weighted according to their masses.
Mathematically, we can write:
${P_{COM}} = \dfrac{{\sum {{P_i}{M_i}} }}{{\sum {{M_i}} }}$
Where ${P_i}$ is the position of ${i^{th}}$ particle,
${M_i}$ is the mass of the ${i^{th}}$ particle and,
${P_{COM}}$ is the position of the Center of mass
Now that we have defined the Center of mass, we can solve the numerical part of the question.
Firstly, we will have to draw the diagram of the given situation, so, we have drawn the diagram below:

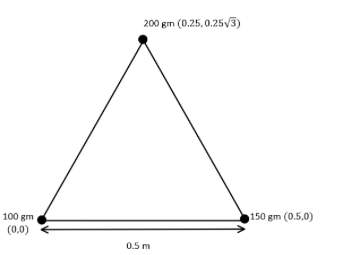
We have taken the particle of mass $100\,gm$ as origin because it was told to us by the question itself.
As for the coordinates of the particle with mass $200\,gm$ we can easily see that its X-coordinate will be half of the length of the side, so $0.25$
For its Y-coordinate, we will need to use Pythagoras theorem to find its Y-coordinate, which we found out to be $0.25\sqrt 3 $
Coordinates of the particle with mass $150\,gm$ can be easily observed to be $\left( {0.5,0} \right)$
Now, we will find the X-coordinate of the Center of mass:
${X_{com}} = \dfrac{{\sum {{x_i}{m_i}} }}{{\sum {{m_i}} }}$
We can write this as:
${X_{com}} = \dfrac{{{x_1}{m_1} + {x_2}{m_2} + {x_3}{m_3}}}{{{m_1} + {m_2} + {m_3}}}$
Substituting the values that we found out:
${X_{com}} = \dfrac{{\left( 0 \right) \times 100 + \left( {0.5} \right)150 + \left( {0.25} \right)200}}{{100 + 150 + 200}}$
Solving this equation, we get:
$
  {X_{com}} = \dfrac{{75 + 50}}{{450}} \\
  {X_{com}} \approx 0.28\,m \\
 $
Now, we need to find the value of Y-coordinate of the Center of mass:
${Y_{com}} = \dfrac{{\sum {{y_i}{m_i}} }}{{\sum {{m_i}} }}$
We can write this as following:
${Y_{com}} = \dfrac{{{y_1}{m_1} + {y_2}{m_2} + {y_3}{m_3}}}{{{m_1} + {m_2} + {m_3}}}$
Substituting in the values that we found out, we get:
${Y_{com}} = \dfrac{{\left( 0 \right)100 + \left( 0 \right)150 + \left( {0.25\sqrt 3 } \right)200}}{{100 + 150 + 200}}$
Upon further solving, we get:
$
  {Y_{com}} = \dfrac{{86.60}}{{450}} \\
  {Y_{com}} = 0.192\,m \\
  {Y_{com}} \approx 0.2\,m \\
 $
Now, we have found out the Y-coordinate of the Center of mass.
The coordinates of Center of mass are $\left( {0.28,0.2} \right)$ .

Note:Your answer may vary from ours if you put the second particle in place where we put our third particle and vice-versa. Main thing is to always put the particle with mass $100\,gm$ at the origin because the question has directed us to do that already, and not doing so would directly mark your solution wrong.