Question

How many cubic metres of the earth must be dug out to sink a well 22.5 m deep and and of diameter, 7 m. Also find the cost of plastering the inner curved surface at Rs.3 per square metre?

Answer 1

Hint: To find the amount of earth needed to be dug out we need to find the volume of the cylinder and the volume is given by $Volume = \pi {r^2}h{{ }}cu.units$ and as we are asked to find the cost of plastering the inner curved surface area. We can find the curved surface area of the cylinder using the formula $CSA = 2\pi rh{{ }}sq.units$ and multiplying it by 3 we get the required cost.

Complete step by step solution:
We are asked to find the amount of earth to be dug to sink a well.
We know that a well is dug in a shape of a cylinder with diameter 7 m and height 22.5 m.

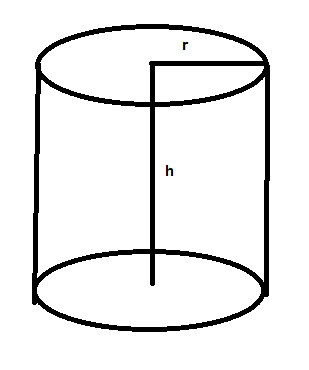
In order to calculate the amount of earth needed to be dug out we need to find the volume of the well.
So now from the given details we have
$
   \Rightarrow Diameter,d = 7m \\
   \Rightarrow Height,h = 22.5m \\
 $
We known that the diameter is twice the radius so the radius of the cylinder is given by
$ \Rightarrow r = \dfrac{d}{2} = \dfrac{7}{2}m$
Now the volume of the cylinder is given by
$ \Rightarrow Volume = \pi {r^2}h{{ }}cu.units$
Using the known values we get
$
   \Rightarrow Volume = \dfrac{{22}}{7}{{\times }}\dfrac{7}{2}{{\times }}\dfrac{7}{2}{{\times 22}}{{.5}}{m^3} \\
   \Rightarrow Volume = 11{{\times }}\dfrac{7}{2}{{\times 22}}{{.5}}{m^3} \\
   \Rightarrow Volume = \dfrac{{77}}{2}{{\times 22}}{{.5}}{m^3} \\
   \Rightarrow Volume = 38.5{{\times 22}}{{.5}}{m^3} \\
   \Rightarrow Volume = 866.25{m^3} \\
 $
Therefore the amount of earth to be dug out is $866.25{m^3}$
Now we need to find the amount of plastering the inner curved surface area
The curved surface area of a cylinder is given by the formula
$ \Rightarrow CSA = 2\pi rh{{ }}sq.units$
Now using the known values we get the area to be plastered to be
 $
   \Rightarrow CSA = 2\times \dfrac{{22}}{7}{{\times }}\dfrac{7}{2}{{\times 22}}{{.5}}{m^2} \\
   \Rightarrow CSA = 22{{\times 22}}{{.5}}{m^2} \\
   \Rightarrow CSA = 495{m^2} \\
 $
Therefore the area to be plastered is $495{m^2}$
We are given that cost of plastering one square metre is Rs.3
Hence the cost of plastering $495{m^2}$is
$ \Rightarrow 495 \times 3 = 1485$

Therefore the cost of plastering is Rs.1485.

Note :
We always need to have a careful eye on the units on the given dimensions and make sure everything is of the same units. After getting the same unit only we can move further for the calculations.