Question

Construct $\vartriangle PQR$ if $PQ = 5cm$, $m\angle PQR = {105^ \circ }$ and $m\angle QRP = {40^ \circ }$.

Answer 1

Hint: Angle Sum Property: In a triangle, the sum of all the three angles of a triangle is equal to ${180^ \circ }$. For example, in a triangle $ABC$, $\angle A,\angle B$ and $\angle C$ are the three angles of this triangle $ABC$.
Then, the angle sum property states that
\[ \Rightarrow \]$\angle A + \angle B + \angle C = {180^ \circ }$
This property is used where two angles of a triangle are given and we can find out the third one with the help of this.
We will make a rough diagram of the triangle and then with the help of geometrical instruments, we will measure them and then draw them.

Complete step-by-step answer:
Firstly, we will draw a rough diagram of $\vartriangle PQR$ where $PQ = 5cm$, $\angle PQR = {105^ \circ }$ and $\angle PRQ = {40^ \circ }$

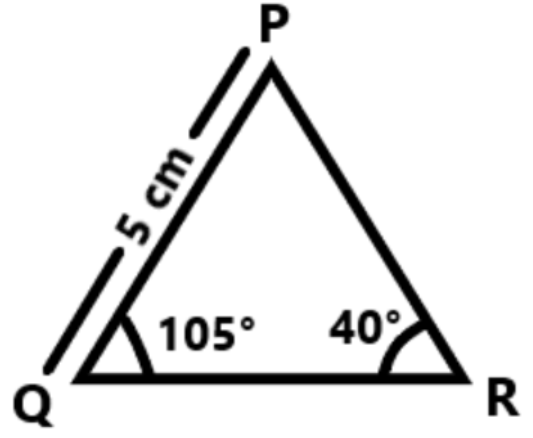
Using angle sum property, we can find the third angle.
\[ \Rightarrow \]$\angle PQR + \angle PRQ + \angle QPR = {180^ \circ }$
\[ \Rightarrow \]${105^ \circ } + {40^ \circ } + \angle QPR = {180^ \circ }$
\[ \Rightarrow \]$\angle QPR = {180^ \circ } - {105^ \circ } - {40^ \circ } = {35^ \circ }$
$\therefore \angle QPR = {35^ \circ }$
Now make a line segment $PQ = 5cm$, then from $P$, make an arc of ${35^ \circ }$ and from $Q$ make an arc of ${105^ \circ }$. The point where these two arcs meet is point $R$ which is equal to ${40^ \circ }$.
Hence, $\vartriangle PQR$ is constructed in which $PQ = 5cm$, $\angle RPQ = {35^ \circ }$, $\angle PQR = {105^ \circ }$ and $\angle PRQ = {40^ \circ }$

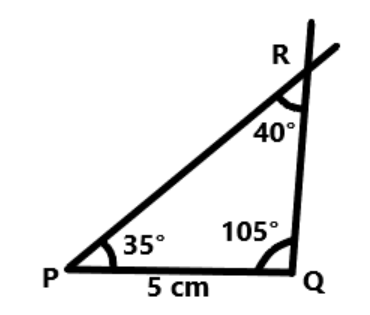
Note: Angles made in a triangle can be made either by Dee (geometrical instrument) or by a protector.
After constructing the triangle PQR, check the angle $\angle PRQ$. It should be equal to ${40^ \circ }$; if it is ${40^ \circ }$, then our constructed triangle is correct, otherwise incorrect.