Question

Construct a triangle XYZ in which $\angle Y={{30}^{\circ }}$,$\angle Z={{90}^{\circ }}$and $XY+YZ+ZX=11$cm \[\]

Answer 1

Hint: We draw the line segment AB which represents the perimeter of the triangle XYZ, $XY+YZ+ZX=11$. We construct an angle of ${{30}^{\circ }}$on point A and an angle of ${{60}^{\circ }}$ on the point B which we later bisect to meet at point X. We draw the perpendicular bisector AX which intersects AB on Y and the perpendicular bisector BX which intersects AB on Y. We join XY and XZ to have the required triangle XYZ.\[\]

Complete step-by-step solution
We are given two angles of the triangle XYZ that need to be constructed$\angle Y={{30}^{\circ }}$,$\angle Z={{90}^{\circ }}$ and the sum of lengths of the sides $XY+YZ+ZX=11$cm. \[\]
Step-1: We draw a line segment AB of length $XY+YZ+ZX=11$cm using scale. \[\]

Step-2: We construct angle $\angle LAB={{30}^{\circ }}$ on the point A by first constructing ${{60}^{\circ }}$ by taking an arc with the compass and then bisecting the angle of ${{60}^{\circ }}$. We construct angle $\angle MBA={{90}^{\circ }}$by taking the arc of ${{60}^{\circ }}$twice on the point $B$and then bisecting the second arc. \[\]

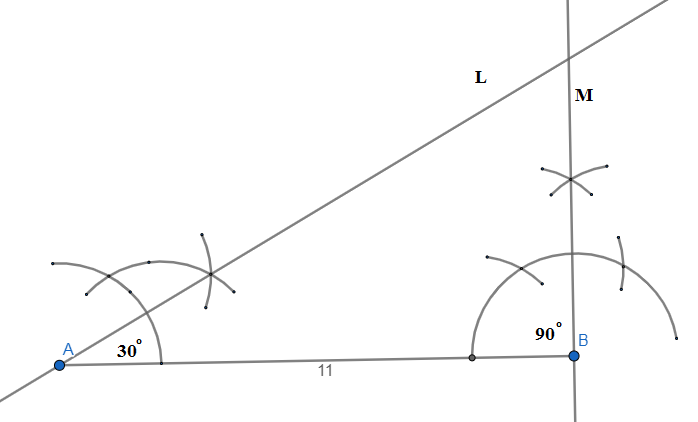
Step-3: We bisect angle $\angle LAB={{30}^{\circ }}$and $\angle MBA={{90}^{\circ }}$ by taking width of the arc of ${{30}^{\circ }},{{90}^{\circ }}$ and using the compass. We denote the point of intersection of bisecting rays of $\angle LAB,\angle MBA$ as $X$.\[\]

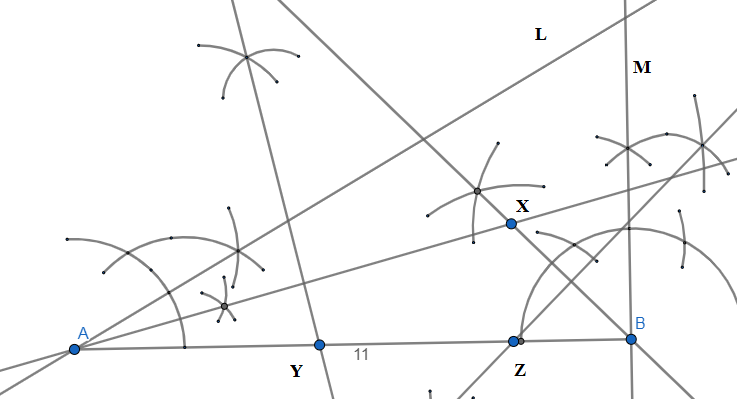
Step-4: We draw the perpendicular bisector of AX and we denote its point of intersection with AB as Y taking the length of AX as an arc using the compass. We similarly draw the perpendicular bisector of BX and denote its point of intersection with AB as Z taking the length of BX as an arc using the compass. \[\]

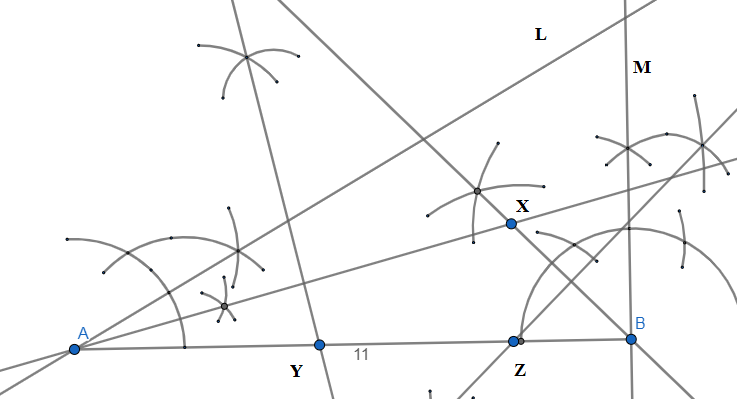
Step-5: We join the line segment XY and YZ using the scale. \[\]
 

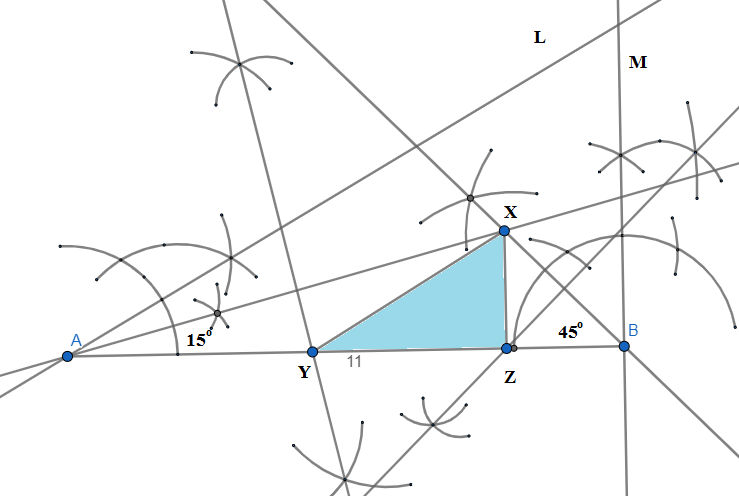
XYZ is the required constructed triangle. \[\]

Note: We can justify the above construction first observing the triangle AYX where Y lies on the perpendicular bisector of AX which gives us $AY=YX\Rightarrow \angle YAX=\angle YXA=\dfrac{{{30}^{\circ }}}{2}={{15}^{\circ }}$ which implies$\angle AYX={{180}^{\circ }}-\left( \angle YAX+\angle YXA \right)={{150}^{\circ }}\Rightarrow \angle XYZ={{30}^{\circ }}$. Similarly Z lies on the perpendicular bisector of AX which gives us $ZX=ZB\Rightarrow \angle ZBX=\angle ZXB={{45}^{\circ }}$ which implies$\angle XZY={{90}^{\circ }}$. We also have $XY+YZ+ZX=AY+YZ+ZB=11$cm.