Question

Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.

Answer 1

Hint:Draw two concentric circles of radius 4 cm and 6 cm. take a point B on the outer circle and join it to the centre O. Find the centre C of OB. Take C as centre and OC as radius, draw a circle. This circle intersects the 4 cm circle at P and Q. Join BP and BQ to get the required tangents. Measure them. To verify, use Pythagoras theorem on triangle BPO to find the length of BP and compare it with the measured length.

Complete step-by-step answer:
In this question, we need to construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also, we need to verify the measurement by actual calculation.
In order to do the desired construction, we follow the following steps:
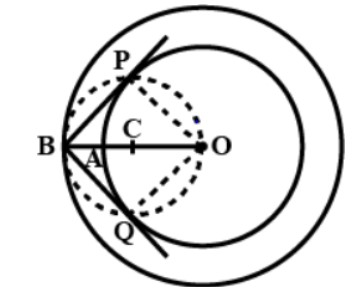
Step 1: Take a point O on the plane of the paper and draw a circle of radius OA = 4 cm. Also draw a concentric circle of radius OB = 6 cm.

Step 2: Find the midpoint C of OB by drawing the bisector of OB. Then draw a circle of radius OC = BC and centre at the point C. Suppose this circle intersects the circle of radius 4 cm at P and Q.

Step 3: Join BP and BQ to get the desired tangents from a point B on the circle of radius 6 cm.
By actual measurement, we find the BP = BQ = 4.5 cm.
The following figure shows the final construction where BP and BQ are the required tangents.

Verification by actual calculation:
In triangle BPO, we have OB = 6 cm and OP = 4 cm.
Also, we know that a tangent makes a right angle with a radius of the circle.
So, in the triangle BPO, P is at a right angle.
Now we will apply the Pythagoras theorem in triangle BPO.
$O{{B}^{2}}=B{{P}^{2}}+O{{P}^{2}}$
$B{{P}^{2}}=O{{B}^{2}}-O{{P}^{2}}$
$B{{P}^{2}}=36-16=20$
$BP=\sqrt{20}=4.47$ cm.
Similarly, $BQ=4.47$ cm.
Now, the measured length = 4.5 cm.
The actual theoretical length = 4.47 cm $\simeq $ 4.5 cm.
So the construction is verified by the theoretical calculation.

Note: In this question, it is important to know the concepts of constructions. In step 2, we constructed the bisector of OB. To do this, take O as centre and radius more than half of OB and make arcs on both the sides of the segment OB. Similarly, draw two arcs keeping the radius same as before and B as centre. The arcs will intersect each other on both the sides of the line. Joint the intersection points. This is the perpendicular bisector of OB. The point where it cuts OB is C.