Question

Construct a right angle triangle ABC with hypotenuse $BC=8$cm and $AB=6$ cm \[\]

Answer 1

Hint:
We draw the side $AB=6$cm first with ruler and divider. We construct a right angle at point A with a rounder and then take an arc of 8 cm from point B and denote the point of intersection with a perpendicular line at A as C. We join BC to get the right-angled triangle as ABC. \[\]


Complete step by step answer:
Step-1: We draw the side $AB=6$ using the scale . \[\]

Step-2: We construct at the right angle at point A. We use the compass and take a semi-circular arc of length about less than half of AB to cut AB at any point say P. \[\]

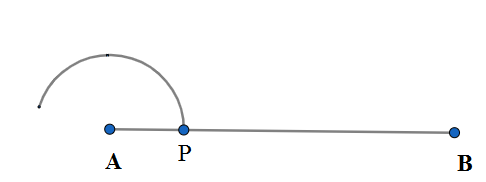
Step-3: We take the same arc length and cut semi-circular at two points say Q and R which denotes to arc angle measure${{60}^{\circ }},{{120}^{\circ }}$. \[\]

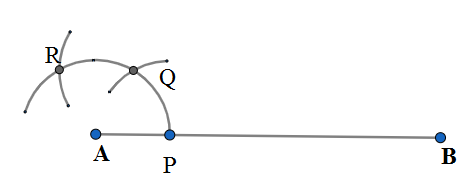
Step-4:We bisect the arc between ${{60}^{\circ }},{{120}^{\circ }}$arcs taking arc of length at Q and R and point of intersection an S. We join AS and extended as a line. We get the angle $\angle SAB={{90}^{\circ }}$ will our right angle for the triangle. \[\]

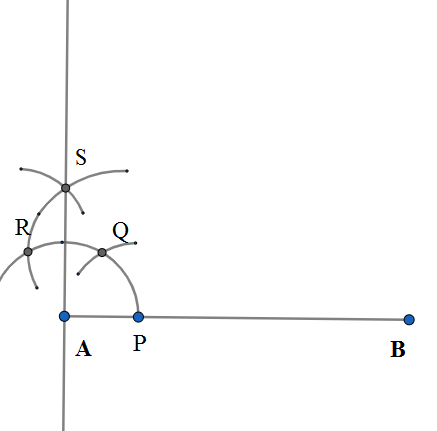
Step-5: We take an arc length of 8 cm from and intersect the line AS . We denote the point as C and then join BC. \[\]

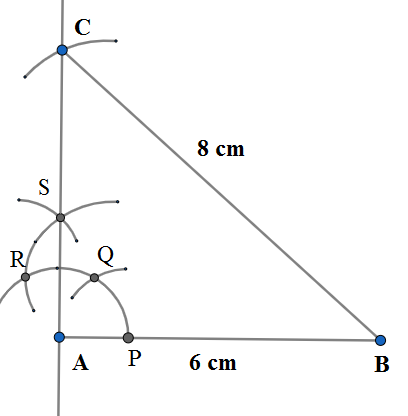
The obtained triangle ABC is the required right-angled triangle. \[\]
Note:
 We note that a triangle is called right-angled when of the angle sic right angle that is the angle of measure${{90}^{\circ }}$. In a right-angled triangle, the side opposite to the right angle is called hypotenuse and hence we have drawn the right angle at A because its opposite side is BC which is given to us as the hypotenuse. We get ${{90}^{\circ }}$bisecting the arcs of ${{60}^{\circ }},{{120}^{\circ }}$because$\dfrac{{{120}^{\circ }}+{{60}^{\circ }}}{2}=\dfrac{{{180}^{\circ }}}{2}={{90}^{\circ }}$. We can also directly bisect straight angles to get the right angle.