
Compare the following numbers.
A. $ - 7, - 2$
B. $0,\dfrac{{ - 9}}{5}$
C. $\dfrac{{ - 17}}{{20}},\dfrac{{ - 13}}{{20}}$
D. $\dfrac{{15}}{{12}},\dfrac{7}{{16}}$
Answer
551.1k+ views
Hint: We are given numbers and we have compare them and have to find out which is smaller number and which is the bigger number, we can use the concept of the number line to compare the numbers, the numbers can be represented in a number, when marked on a number line greater numbers lie toward right and smaller lie towards left. If a number lies with respect to another number we can say, the former number is smaller than the latter.
Complete answer:
We are given four pairs of numbers, for each pair, we have to find the smaller one. We can use a number line to compare the numbers. 0 is considered as the centre of the number line.
Positive numbers are marked towards the right of the zero and negative numbers are marked towards the left of the 0.
The value of the number will increase as the distance from zero increases.
Both the given numbers are negative, we have to find the least and greatest negative numbers.
Now using the number line, we can compare the given two numbers.
Now drawing the number line,
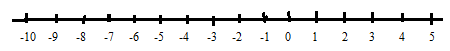

From the number line we can say that negative numbers increase in magnitude when distance from zero increases, so in two negative numbers the number with larger magnitude is the smaller number.
So from the number line it is clear that $ - 7$ is far from zero and $ - 2$ is near to zero, and $ - 2$ is in the right of \[ - 7\], so\[ - 2\] is greater than\[ - 7\].
So \[ - 2 > - 7\]
2. Given numbers are $0,\dfrac{{ - 9}}{5}$,

From the number line we can say that negative numbers increase in magnitude when distance from zero increases, so in two negative numbers the number with larger magnitude is the smaller number.
So from the number line it is clear that $ - \dfrac{9}{5}$ is far from zero and the second number is itself \[0\] as it is considered as the centre of the number line, and \[0\] is in the right of $ - \dfrac{9}{5}$,\[0\] is greater than \[\dfrac{{ - 9}}{5}\].
So \[0 > - \dfrac{9}{5}\].
3. Given numbers are $\dfrac{{ - 17}}{{20}},\dfrac{{ - 13}}{{20}}$,
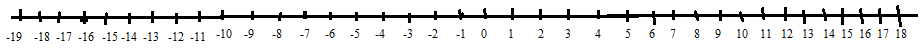
From the number line we can say that negative numbers increase in magnitude when distance from zero increases, so in two negative numbers the number with larger magnitude is the smaller number.
Here numbers are rational numbers which are fractions and they have the same denominator but different numerators. In these types of questions if denominators are equal, compare the numerators and here numerators are\[ - 17\] and \[ - 13\], here \[ - 17\] will be a smaller number then compared to \[ - 13\].
So from the number line it is clear that \[ - 17\] is far from zero and the \[ - 13\] is near to \[0\] and \[ - 13\] is in the right of \[ - 17\], \[ - 13\] is greater than \[ - 17\].
So \[\dfrac{{ - 17}}{{20}} < \dfrac{{ - 13}}{{20}}\]
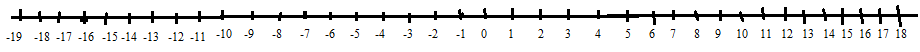
Here numbers are rational numbers which are fractions and they have different denominators and different numerators. In these type of questions if denominators are different, we have to take the L.C.M of the denominators, now simplifying the first number we get,\[ \Rightarrow \dfrac{3}{4},\dfrac{7}{{16}}\]
Now the denominators are \[4\] and $16$ now taking the L.C.M of \[4\] and $16$we will get $16$,now the numbers become,\[ \Rightarrow \dfrac{{12}}{{16}},\dfrac{7}{{16}}\],
$12$ Now the numbers have the same denominator but different numerator. In these types of questions if denominators are equal, compare the numerators and here numerators are $12$ and \[7\].
So from the number line it is clear that $12$ is far from zero and the is near to \[0\] and $12$ is in the right of \[7\],$12$ is greater than \[7\].
So \[\dfrac{{15}}{{12}} > \dfrac{7}{{16}}\].
Final Answer:
1. \[ - 2 > - 7\].
2. \[0 > - \dfrac{9}{5}\].
3. \[\dfrac{{ - 17}}{{20}} < \dfrac{{ - 13}}{{20}}\].
4. \[\dfrac{{15}}{{12}} > \dfrac{7}{{16}}\].
Note:
We have to find the points A, B and C to plot the graph of the given equation of line $y - 2x = 4$ we can be determined by substituting $x = 0,1, - 2$ in the given equation of line.
To satisfy that the points $(2,8)$ and $(4,2)$ lies on the given equation of line $y - 2x = 4$ by substituting $x = 2,y = 8$ and $x = 4,y = 2$ in the given equation of line $y - 2x = 4$.
Complete answer:
We are given four pairs of numbers, for each pair, we have to find the smaller one. We can use a number line to compare the numbers. 0 is considered as the centre of the number line.
Positive numbers are marked towards the right of the zero and negative numbers are marked towards the left of the 0.
The value of the number will increase as the distance from zero increases.
Both the given numbers are negative, we have to find the least and greatest negative numbers.
Now using the number line, we can compare the given two numbers.
Now drawing the number line,
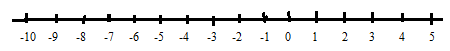
- (1) Given numbers are $ - 7, - 2$,

From the number line we can say that negative numbers increase in magnitude when distance from zero increases, so in two negative numbers the number with larger magnitude is the smaller number.
So from the number line it is clear that $ - 7$ is far from zero and $ - 2$ is near to zero, and $ - 2$ is in the right of \[ - 7\], so\[ - 2\] is greater than\[ - 7\].
So \[ - 2 > - 7\]
2. Given numbers are $0,\dfrac{{ - 9}}{5}$,

From the number line we can say that negative numbers increase in magnitude when distance from zero increases, so in two negative numbers the number with larger magnitude is the smaller number.
So from the number line it is clear that $ - \dfrac{9}{5}$ is far from zero and the second number is itself \[0\] as it is considered as the centre of the number line, and \[0\] is in the right of $ - \dfrac{9}{5}$,\[0\] is greater than \[\dfrac{{ - 9}}{5}\].
So \[0 > - \dfrac{9}{5}\].
3. Given numbers are $\dfrac{{ - 17}}{{20}},\dfrac{{ - 13}}{{20}}$,
From the number line we can say that negative numbers increase in magnitude when distance from zero increases, so in two negative numbers the number with larger magnitude is the smaller number.
Here numbers are rational numbers which are fractions and they have the same denominator but different numerators. In these types of questions if denominators are equal, compare the numerators and here numerators are\[ - 17\] and \[ - 13\], here \[ - 17\] will be a smaller number then compared to \[ - 13\].
So from the number line it is clear that \[ - 17\] is far from zero and the \[ - 13\] is near to \[0\] and \[ - 13\] is in the right of \[ - 17\], \[ - 13\] is greater than \[ - 17\].
So \[\dfrac{{ - 17}}{{20}} < \dfrac{{ - 13}}{{20}}\]
- 1. Given numbers are$\dfrac{{15}}{{12}},\dfrac{7}{{16}}$,
Here numbers are rational numbers which are fractions and they have different denominators and different numerators. In these type of questions if denominators are different, we have to take the L.C.M of the denominators, now simplifying the first number we get,\[ \Rightarrow \dfrac{3}{4},\dfrac{7}{{16}}\]
Now the denominators are \[4\] and $16$ now taking the L.C.M of \[4\] and $16$we will get $16$,now the numbers become,\[ \Rightarrow \dfrac{{12}}{{16}},\dfrac{7}{{16}}\],
$12$ Now the numbers have the same denominator but different numerator. In these types of questions if denominators are equal, compare the numerators and here numerators are $12$ and \[7\].
So from the number line it is clear that $12$ is far from zero and the is near to \[0\] and $12$ is in the right of \[7\],$12$ is greater than \[7\].
So \[\dfrac{{15}}{{12}} > \dfrac{7}{{16}}\].
Final Answer:
1. \[ - 2 > - 7\].
2. \[0 > - \dfrac{9}{5}\].
3. \[\dfrac{{ - 17}}{{20}} < \dfrac{{ - 13}}{{20}}\].
4. \[\dfrac{{15}}{{12}} > \dfrac{7}{{16}}\].
Note:
We have to find the points A, B and C to plot the graph of the given equation of line $y - 2x = 4$ we can be determined by substituting $x = 0,1, - 2$ in the given equation of line.
To satisfy that the points $(2,8)$ and $(4,2)$ lies on the given equation of line $y - 2x = 4$ by substituting $x = 2,y = 8$ and $x = 4,y = 2$ in the given equation of line $y - 2x = 4$.
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
What is the Full Form of ISI and RAW

What is the role of Mahatma Gandhi in national movement

What is the difference between Atleast and Atmost in class 9 maths CBSE

What were the main changes brought about by the Bolsheviks class 9 social science CBSE

Differentiate between the Western and the Eastern class 9 social science CBSE

Differentiate between parenchyma collenchyma and sclerenchyma class 9 biology CBSE





