Question

Calculate the area and perimeter of a quadrant of a circle of radius 21 cm.

Answer 1

Hint: A quadrant is a quarter of a circle. First work out the area of the whole circle and then divide the answer by 4. Second work out the perimeter of the whole circle, then divide by 4 and add length of the two sides.

Complete step-by-step solution -

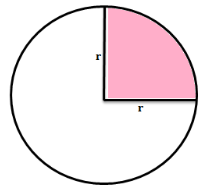
First work out the area of the whole circle by substituting the radius of r = 21 cm into the formula for the area of the circle.
The area of the circle $=\pi \times {{r}^{2}}.............(1)$
The area of the circle $=\pi \times {{(21)}^{2}}$
Put the value of the $\pi =\dfrac{22}{7}$ in the equation (1), we get
The area of the circle $=\dfrac{22}{7}\times 441=3.142\times 441=1385.62$
A quadrant is one-fourth of a circle. If a circle is evenly divided into four sections by two perpendicular lines, then each of the four areas is a quadrant.

So the area of the circle is divided by 4.
The area of a quadrant of the circle $=\dfrac{1385.62}{4}=346.40$
Hence the area of a quadrant of the circle is 346. 40 $c{{m}^{2}}$.
Second work out the perimeter of the whole circle by substituting the radius of r = 21 cm into the formula for the circumference of the circle.
The circumference of the circle $=2\pi r.................(2)$
The circumference of the circle $=2\pi (21)$
Put the value of the $\pi =\dfrac{22}{7}$ in the equation (2), we get
The circumference of the circle $=2\times \dfrac{22}{7}\times (21)=2\times 3.142\times 21=131.96$
A quadrant of a circle is a sector of the circle whose sectorial angle is 90 degree.
The perimeter of a quadrant of the circle is one fourth of the circumference and 2 times of the radius of the circle.
The perimeter of a quadrant of the circle $=\dfrac{2\pi r}{4}+2(r)$
The perimeter of a quadrant of the circle $=\dfrac{131.96}{4}+2(21)$
The perimeter of a quadrant of the circle $=\dfrac{131.96}{4}+42=74.99=75$
Hence the perimeter of a quadrant of the circle is 75 cm.

Note: Alternatively, you could substitute the radius of the quadrant directly into the formula of area $\left( A=\dfrac{1}{4}\pi {{r}^{2}} \right)$ and perimeter $\left[ P=\left( \dfrac{\pi }{2}+2 \right)r \right]$ of a quadrant of the circle.