Question

Assume that we are filling wheat from bags into a circular drum of radius 4.2 m and height 3.5 m, find how many full bags of wheat can be emptied if the space required for wheat in each bag is 2.1 cubic m.

Answer 1

Hint: We start solving the problem by using the area of the base of the circular radius by using the given radius. After solving the area of the base, we use the height and calculate the volume of the circular drum. We divide the volume of the circular drum by dividing with the volume of a single wheat bag to get the required answer.

Complete step-by-step answer:
We have given a circular drum of radius 4.2 m and height 3.5 m. It (circular drum) is filled with wheat, which were emptied from wheat bags. We need to find the number of bags emptied, if the square required for wheat in each bag is $ 2.1{{m}^{3}} $ .
We have a circular drum as shown in the figure,

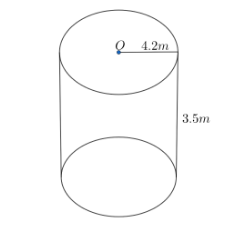
Before calculating the no. of bags emptied, we find the volume of the circular drum.
We find the area of the base of the circular drum in order to find the volume of the drum.
We have a base of circular drums with a radius of 4.2 m.
We know that area (A) of the circle of radius ‘r’ is $ A=\pi {{r}^{2}} $ .
Now area $ \left( {{A}_{1}} \right) $ of the base of circular drum is $ {{A}_{1}}=\pi \times {{\left( 4.2 \right)}^{2}} $ .
We take the approximate value $ \pi =\dfrac{22}{7} $ .
We have $ {{A}_{1}}=\dfrac{22\times 4.2\times 4.2}{7} $ .
We have $ {{A}_{1}}=22\times 4.2\times 0.6 $ .
We have $ {{A}_{1}}=55.44{{m}^{2}} $ .
We know that volume (V) of a material with area ‘A’ and height ‘h’ is defined as $ V=A\times h $ .
We have volume $ \left( {{V}_{1}} \right) $ of the drum, $ {{V}_{1}}={{A}_{1}}\times 3.5 $ .
 $ {{V}_{1}}=55.44\times 3.5 $ .
 $ {{V}_{1}}=194.04{{m}^{3}} $ .
Now we need to find the no. of wheat bags that can be emptied. We have the volume of each bag as $ 2.1{{m}^{3}} $ .
No. of bags emptied = $ \dfrac{\text{volume of drum}}{\text{volume of each bag}} $ .
No. of bags emptied = $ \dfrac{194.04}{2.1} $ .
No. of bags emptied = $ 92.4 $ .
We take an approximation as 92 bags.
∴ The total bags can be emptied are 92 bags.

Note: We assume the value of $ \pi $ as $ \dfrac{22}{7} $ for easier calculation purposes. But we also use the value $ 3.14 $ in place of $ \pi $ . We should not confuse the volume of this drum with the volume of the cylinder. We always approximate the no. of bags with the natural number that is just less than the obtained value. As they can be completely emptied.