
What is the area of the sector?
A. $ 170\,c{{m}^{2}} $
B. $ 100\,c{{m}^{2}} $
C. $ 110\,c{{m}^{2}} $
D. $ 130\,c{{m}^{2}} $

Answer
491.1k+ views
Hint: Here we have to find the area of the sector given. Firstly we will write down all the information like the angle of the sector, its radius or diameter which of them is given in the diagram. Then we will write the formula used for finding the area of a sector. Finally we will substitute all the values in the formula and solve it to get the desired answer.
Complete step-by-step answer:
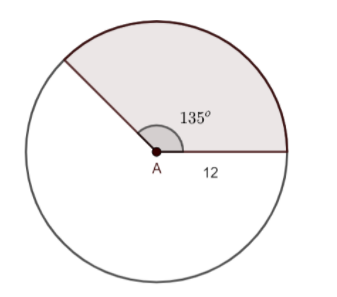
The diagram of the circle and the sector in it is given as follows:
The information given in the diagram is as follows:
Angle of sector $ \theta ={{135}^{\circ }} $ …. $ \left( 1 \right) $
Radius of the circle $ r=12\,cm $ …… $ \left( 2 \right) $
The area of the sector is calculated by the below formula:
$ A=\left( \dfrac{\theta }{{{360}^{\circ }}} \right)\times \pi {{r}^{2}} $
On substitute the values from equation (1) and (2) in above formula we get,
$ A=\left( \dfrac{{{135}^{\circ }}}{{{360}^{\circ }}} \right)\times \pi {{\left( 12\,cm \right)}^{2}} $
Put $ \pi =\dfrac{22}{7} $ and solve as follows:
$ \Rightarrow A=\left( \dfrac{{{135}^{\circ }}}{{{360}^{\circ }}} \right)\times \dfrac{22}{7}\times {{\left( 12\,cm \right)}^{2}} $
$ \Rightarrow A=\left( \dfrac{{{9}^{\circ }}}{{{24}^{\circ }}} \right)\times \dfrac{22}{7}\times 144\,c{{m}^{2}} $
Simplifying them completely we get,
$ A=169.71\,c{{m}^{2}} $
Approximately we can write the value as,
$ A\approx 170\,c{{m}^{2}} $
So, the correct answer is “Option A”.
Note: A sector is a pie-shaped part of a circle which is made up of the arc of the circle along with the two radii of the circle. It looks like a pizza slice or as the name suggests like a pie. In it the simplest shape in geometry it has various parts such as diameter, radius, circumference, sector and segment. The circle is divided into two sectors the bigger part is known as the major sector while the smaller part is known as the minor sector. A special case when a circle is divided into two equal parts is known as a semi-circle.
Complete step-by-step answer:
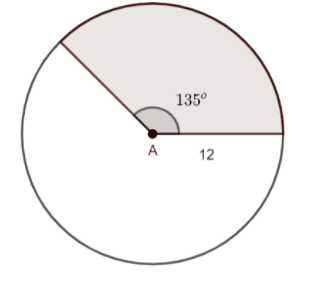
The diagram of the circle and the sector in it is given as follows:

The information given in the diagram is as follows:
Angle of sector $ \theta ={{135}^{\circ }} $ …. $ \left( 1 \right) $
Radius of the circle $ r=12\,cm $ …… $ \left( 2 \right) $
The area of the sector is calculated by the below formula:
$ A=\left( \dfrac{\theta }{{{360}^{\circ }}} \right)\times \pi {{r}^{2}} $
On substitute the values from equation (1) and (2) in above formula we get,
$ A=\left( \dfrac{{{135}^{\circ }}}{{{360}^{\circ }}} \right)\times \pi {{\left( 12\,cm \right)}^{2}} $
Put $ \pi =\dfrac{22}{7} $ and solve as follows:
$ \Rightarrow A=\left( \dfrac{{{135}^{\circ }}}{{{360}^{\circ }}} \right)\times \dfrac{22}{7}\times {{\left( 12\,cm \right)}^{2}} $
$ \Rightarrow A=\left( \dfrac{{{9}^{\circ }}}{{{24}^{\circ }}} \right)\times \dfrac{22}{7}\times 144\,c{{m}^{2}} $
Simplifying them completely we get,
$ A=169.71\,c{{m}^{2}} $
Approximately we can write the value as,
$ A\approx 170\,c{{m}^{2}} $
So, the correct answer is “Option A”.
Note: A sector is a pie-shaped part of a circle which is made up of the arc of the circle along with the two radii of the circle. It looks like a pizza slice or as the name suggests like a pie. In it the simplest shape in geometry it has various parts such as diameter, radius, circumference, sector and segment. The circle is divided into two sectors the bigger part is known as the major sector while the smaller part is known as the minor sector. A special case when a circle is divided into two equal parts is known as a semi-circle.
Recently Updated Pages
Questions & Answers - Ask your doubts

A man running at a speed 5 ms is viewed in the side class 12 physics CBSE

State and explain Hardy Weinbergs Principle class 12 biology CBSE

Which of the following statements is wrong a Amnion class 12 biology CBSE

Two Planoconcave lenses 1 and 2 of glass of refractive class 12 physics CBSE

The compound 2 methyl 2 butene on reaction with NaIO4 class 12 chemistry CBSE

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is the Full Form of ISI and RAW

Golden Revolution is related to AFood production BOil class 9 social science CBSE





