Question

Area of a square is $16200{{m}^{2}}$. Find the length of its diagonals.

Answer 1

Hint: In this question, we are given the area of a square and we have to find the length of its diagonals. For this, we will draw a figure for better understanding. We will use the formula of finding the area of the square when the side is given and Pythagoras theorem to find our required answer. Area of square $={{s}^{2}}$, where $s$ represents side of a square. Pythagoras theorem states that the sum of squares of base and perpendicular is equal to square of hypotenuse.

Complete step by step answer:
Here, we are given the area of a square as $16200{{m}^{2}}$ and we have to find the length of its diagonals. Let us draw a figure for better understanding.

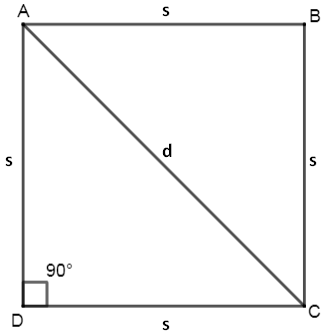
As we know, in a square all sides are equal and adjacent sides are perpendicular to each other. Also, diagonal is a line formed by joining any two opposite vertices. Hence, ACD forms a right angles triangle with right angle at D. We can see this from the figure also.
Now, let us suppose side of a square as $s$$cm$and length of diagonal as $d$$cm$.
Side of a square $=s$$cm$
Length of diagonal $=d$$cm$
In right angles triangle $\Delta ACD$, we can use Pythagoras theorem according to which, ${{\left( AC \right)}^{2}}={{\left( AD \right)}^{2}}+{{\left( CD \right)}^{2}}$
Here, AC represents the diagonal of the square, and AD, CD represents two sides of a square. Therefore,
$\begin{align}
  & {{\left( d \right)}^{2}}={{\left( s \right)}^{2}}+{{\left( s \right)}^{2}} \\
 &\Rightarrow {{\left( d \right)}^{2}}=2{{\left( s \right)}^{2}} \\
\end{align}$
Taking square root both sides, we get –
$\begin{align}
  & d=\sqrt{2}s \\
 &\Rightarrow s=\dfrac{d}{\sqrt{2}}~~~~~~~~~~...(1) \\
\end{align}$
As we know, area of square $={{\left( side \right)}^{2}}$
Therefore, area of square $={{s}^{2}}$
From (1), let us put the value of $s$. We will get –
Area of square $={{\left( \dfrac{d}{\sqrt{2}} \right)}^{2}}$
But we also know, value of area of square as $16200{{m}^{2}}$, therefore
$\begin{align}
  & 16200={{\left( \dfrac{d}{\sqrt{2}} \right)}^{2}} \\
 &\Rightarrow 16200=\left( \dfrac{{{d}^{2}}}{2} \right) \\
\end{align}$
Cross multiplying, we get –
\[32400={{d}^{2}}\]
Taking square root both sides, we get –
\[d=\sqrt{32400}\]
As we know, we can write
$32400$ as $324\times 100={{2}^{2}}\times {{3}^{2}}\times {{3}^{2}}\times {{10}^{2}}$
Hence, $\sqrt{32400}=2\times 3\times 3\times 10=180$
So, $d=180m$.

Since $d$ was supposed to be the length of diagonal of square, therefore,
Diagonal of the square $=180m$.

Note: Students can also use direct formula for finding area of square using length of diagonals which is given as, area of square $=\dfrac{{{\left( diagonal \right)}^{2}}}{2}$. This formula is derived from the area of rhombus whereas the area of rhombus was equal to the product of both diagonals divided by $2$. Since, the square is a special case of rhombus, so we can directly use this formula also. Students should take care while calculating square roots of values. Also take care while applying Pythagoras theorem.