Question

Area of 4 walls of a cuboid is 448 sq.cm, its length is 18 cm and height is 8 cm. What is its breadth (in cm)?
$
  A.{\text{ 10}} \\
  B.{\text{ 9}} \\
  C.{\text{ 8}} \\
  D.{\text{ 7}} \\
 $

Answer 1

Hint: Here we go through by assuming the diagram of cuboid and then apply the formula of area of four walls of cuboid then put the values that are given in the formula then find out the unknown terms.

Complete step-by-step answer:
First method
For clear understanding what the area of 4 walls of cuboid is we draw its diagram.

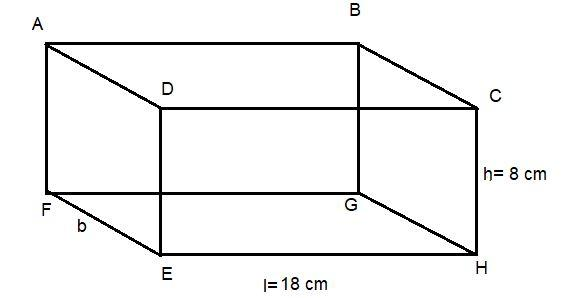
Here the area of 4 walls of cuboid means the sum of the area of face, ADEF, CDEH, BCGH and ABFG.
And we see that these faces are in the shape of a rectangle in which the face ADEF and face BCGH are the same with length =8cm and breadth= b and the other two faces CDEH and ABFG are same with length l= 18cm and height h= 8cm.
And we know that area of rectangle is $l \times b$
Then for the area of face ADEF and face BCGH we apply this formula we get,
Area of face ADEF and face BCGH $ = 2 \times 8 \times b = 16b{\text{ }}c{m^2}$
Similarly area of faces CDEH and ABFG$ = 2 \times 18 \times 8 = 288{\text{ }}c{m^2}$
And the total area of these four surfaces is given as 448$c{m^2}$
i.e. 16b+288=448$c{m^2}$
$
   \Rightarrow 16b = 448 - 288 \\
   \Rightarrow b = \dfrac{{160}}{{16}} = 10cm \\
 $
Second method
And the simple method that we use generally is by applying the formula of area of 4 walls of cuboid i.e. $2(l + b) \times h$.
Area of 4 walls of cuboid=$2(l + b) \times h$
After putting the values in formula we get,
$
   \Rightarrow 448 = 2(18 + b) \times 8 \\
   \Rightarrow 224 = 18 \times 8 + 8b \\
   \Rightarrow 224 - 144 = 8b \\
   \Rightarrow b = \dfrac{{80}}{8} = 10cm \\
 $
Hence the breadth is equal to 10 cm.

Note: Whenever we face such type of question the key concept for solving the question is just simply put the formula of the area of 4 wall of cuboid and put the terms that are given in the question and find out the unknown terms form that formula and whenever you forgot the formula you can solve as in that manner that I solve in first method.