Question

Why are there \[2\] pi radians in a circle ?

Answer 1

Hint: In this question, we need to explain why there are \[2\] pi radians in a circle. Here pie is nothing but a mathematical constant \[\pi\]. First, let us know the concept and definition of a circle and its circumference. Then by using the definition of revolution, that is, the angle formed in completing a full revolution is equal to the ratio of the circumference of the circle to the radius of the circle , we can tell there are \[2\] pi radians in the circle.

Complete step-by-step answer:
Now let us see some common definitions.
Circle : Circle is nothing but a kind of ellipse in which all the points are equidistant from the centre point. Mathematically, the radius of the circle is represented as \[r\] and the diameter of the circle is \[2r\] .
Circumference : Circumference is nothing but the distance around the circle. The circumference of the circle is the product of mathematical constants and the diameter of the circle.
\[\text{Circumference}\ = \ 2\pi r\]

Also, the circumference is the arc length of the circle as if it opened out to a line segment.
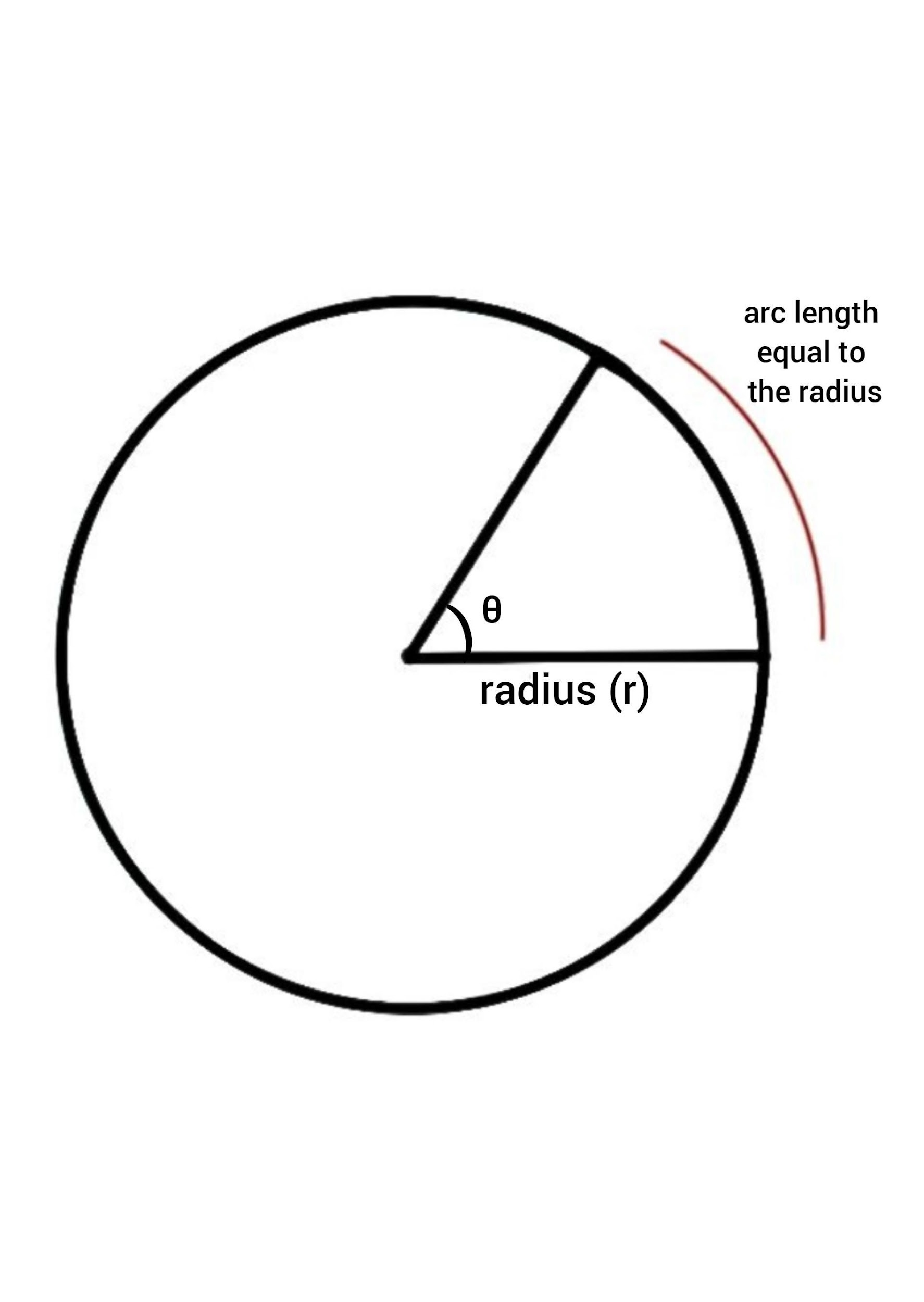
Radian : Radian is nothing but the angle that an arc the same length as the radius of the circle will make.
Now we need to find an angle formed in one complete revolution of the circle .
From the definition of revolution, the total turn of anybody along its circumference which is equal to the circumference of the body i.e. known as the angular displacement of the body.
That is \[\text{angle}\ = \dfrac{\text{arc}}{\text{radius}}\]
Let the angle formed in completing a full revolution be \[\theta\].
Here, arc is nothing but the total angular displacement in one revolution which is the circumference of the circle. That arc is the total circumference of the circular path.
That is \[\text{angle}\ = \dfrac{\text{circumference}}{\text{radius}}\]
On substituting the values of the angle, circumference and radius,
We get,
\[\Rightarrow \ \theta = \dfrac{2\pi r}{r}\]
On simplifying,
We get,
\[\Rightarrow \ \theta = 2\pi\]
Hence we can tell that there are \[2\] pi radians in a circle.
Thus we can say that a full circle or one complete revolution of the circle corresponds to an angle of \[2\pi\] radians.

Final answer :
There are \[2\] pi radians in a circle because of the definition of radian measure.

Note: We need to know that in a circle when a line a drawn from the centre to any point on the circle then that line is known as the radius of the circle similarly when a line is drawn from a end point to the other end point of the circle passing through the centre of the circle is known as diameter of a circle. \[\pi\] (pi) is a special mathematical constant and the value of the mathematical constant is \[3.14\] . Also, we need to know that the revolutions per minute and revolutions per second are the main units of describing frequency of a moving particle in circular motions.