Question

Anshul moves towards East a distance of 5 meters, then he turns to his left and walks 20 meters, then again he turns left and walks 15 meters. Now, he turns ${45^0}$ towards his right and goes straight to cover $20\sqrt 2 $ meters. How far is he from his starting point?
$
  (1){\text{ 40 m}} \\
  {\text{(2) 30 m}} \\
  {\text{(3) 50 m}} \\
  {\text{(4) 55 m}} \\
 $

Answer 1

Hint: Before starting with the solution, candidates should be aware of the directions where man is traveling through like east, west, north, and south. Below is the detailed diagram included for the direction analysis. In this question, all the directions are given in 90 degrees except one which is making an angle of 45 degrees with the horizontal. To start the solution, first of all, we need to draw the traveling trajectory of the man and use the Pythagoras theorem for the calculation of the distance.

Complete step by step solution:

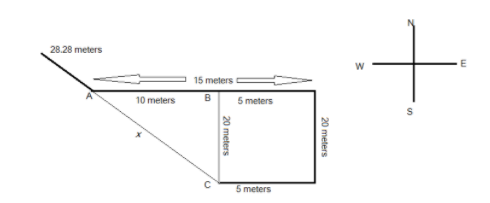
Applying the Pythagoras theorem in the triangle ABC to determine the value of the distance between the points A and X.
Consider the distance between the points A and C be x.
$ A{C^2} = A{B^2} + B{C^2} \\
  {x^2} = {10^2} + {20^2} \\
  {x^2} = 100 + 400 \\
  x = \sqrt {500} \\
   = 10\sqrt 5 \\
   = 10 \times 2.236 \\
   = 22.36{\text{ meters}} \\ $
Now, to calculate the distance between the starting point and the endpoint $20\sqrt 2 = 20 \times 1.414 = 28.28{\text{ meters}}$ will be added to the value 22.36 meters.
$ D = 28.28 + 22.36 \\
   = 50.64{\text{ meters}} \\ $
As we are doing with the approximations in the calculation, the nearest value to the number 50.64 meters given in the option is 50 meters. Hence, the distance between the starting point and the endpoint is 50 meters.

Note: It is very important to note here that, whenever the calculation part includes an approximation then, the value closest to the calculated result will be the desired result. Candidates can remember the direction convention by locating the sun and it is well known that “SUN rises in the EAST” and then follows the direction according to the question.