Question

An angle which measure ${{0}^{\circ }}$ is called,\[\]
A. obtuse \[\]
B. acute angle \[\]
C. zero angle \[\]
D. right angle\[\]

Answer 1

Hint: We recall the definition of angle, measure of an angle as the amount of turn by one ray to coincide another. We recall the definition of degree as a unit of measure of angle and find the relation between degree and turn to choose the correct option for ${{0}^{\circ }}$. \[\]

Complete step by step answer:
We know that angle is a figure formed in the plane by two rays having a common point. The common point is called vertex of the angle and the rays are called sides. If $\overrightarrow{OA},\overrightarrow{OB}$ be two rays that form an angle with vertex O then the angle is denoted $\angle AOB$ whose rough figure is drawn below.\[\]
 

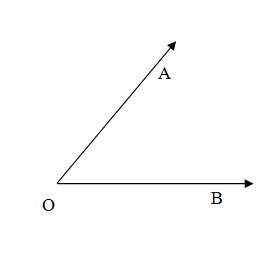
We know that the measure of an angle is the amount of rotation or turn from one ray to another. It is measured as the ratio of length of a circular arc centred at the vertex and bounded by two rays. The measure of angle $\angle AOB$ is amount of turn $\overrightarrow{OB}$ has to complete to coincide with $\overrightarrow{OA}$ or the amount of turn $\overrightarrow{OA}$ has to complete to coincide with $\overrightarrow{OB}$. It is denoted by $m\angle AOB$ or simply $\angle AOB$.
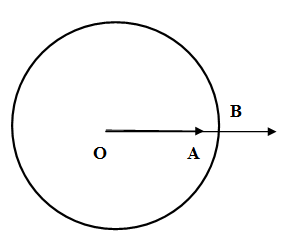
We know that one of the unit of measure of angle is degree. A circle is divided into 360 parts and ${{1}^{\circ }}$ is the amount of turn for ray to cover $\dfrac{1}{360}$ parts of the circle. An angle of measure ${{\theta }^{\circ }}$ is an angle that covers $\theta \times \dfrac{1}{360}=\dfrac{\theta }{360}$ parts of the circle is drawn below. \[\]

If the ray will not turn at all the points $A,B$ will lie in the same line and will cover $\dfrac{0}{360}$ parts of the circle and hence the measure of the angle is ${{0}^{\circ }}$. This angle is also known as zero angle. \[\]
 

So, the correct answer is “Option C”.

Note: We note that if the ray covers ${{\left( \dfrac{1}{4} \right)}^{\text{th}}}$ or quarter of the circle then the angle is called right angle whose measure is ${{360}^{\circ }}\times \dfrac{1}{4}={{90}^{\circ }}$. If ray rotates for ${{\left( \dfrac{1}{2} \right)}^{\text{th}}}$ or half of the circle the angle is called straight angle whose measure is ${{360}^{\circ }}\times \dfrac{1}{2}={{180}^{\circ }}$ If the ray rotates less than quarter of the circle the angle is called with measure less than ${{90}^{\circ }}$ and if the ray rotates more than quarter of the circle but less than half of the circle the angle it is called obtuse angle whose measure is more ${{90}^{\circ }}$ and less than ${{180}^{\circ }}$.