Question

An aeroplane flying horizontally at a height of \[2500m\] above the ground is observed at an elevation of \[{{60}^{\circ }}\]. If after 15 seconds, the angle of elevation is observed to be \[{{30}^{\circ }}\], find the speed of the aeroplane in km per hour.

Answer 1

Hint: We are given a question based on height and distance and we will be using the trigonometric functions to find the required values. We will first draw a diagram using all the given values, so as to get a clear picture of the question. We are asked in the question to find the speed of the given aeroplane as the angle of elevation goes from \[{{60}^{\circ }}\] to \[{{30}^{\circ }}\] in 15 seconds. We will first find the distance covered by the aeroplane in 15 seconds using the appropriate trigonometric functions. Then, we will use the formula of the speed, which is, \[Speed=\dfrac{distance}{time}\]. Hence, we will have the value of the speed of the aeroplane.

Complete step by step answer:
According to the given question, we are given a problem based on the height and distance which is the application of trigonometry. So, we will be using the trigonometric functions to solve the given question.
First of all, we will draw the appropriate diagram with the given values and so we have,

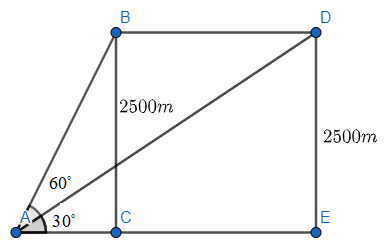
We will now consider the triangle \[\vartriangle ACB\],
We have,
\[\tan {{60}^{\circ }}=\dfrac{BC}{AC}\]
\[\Rightarrow \sqrt{3}=\dfrac{2500}{AC}\]
We get the value of the side AC as,
\[\Rightarrow AC=\dfrac{2500}{\sqrt{3}}m\]
Now, considering the triangle \[\vartriangle AED\],
\[\tan {{30}^{\circ }}=\dfrac{DE}{AE}\]
\[\Rightarrow \tan {{30}^{\circ }}=\dfrac{2500}{AE}\]
\[\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{2500}{AE}\]
Now, we have the value of AE as,
\[\Rightarrow AE=2500\sqrt{3}m\]
Now we have to find the value of CE which in turn is the value of BD as CE and BD are parallel and so have similar values.
\[CE=AE-AC\]
We will now be substituting the values and we get,
\[\Rightarrow CE=2500\sqrt{3}-\dfrac{2500}{\sqrt{3}}\]
\[\Rightarrow CE=\dfrac{2500\left( 3 \right)-2500}{\sqrt{3}}\]
\[\Rightarrow CE=\dfrac{7500-2500}{\sqrt{3}}\]
\[\Rightarrow CE=\dfrac{5000}{\sqrt{3}}m\]
So, we have, \[CE=BD=\dfrac{5000}{\sqrt{3}}m\]
That is, now we have the distance travelled by the aeroplane in 15 seconds which caused the angle of elevation to move from \[{{60}^{\circ }}\] to \[{{30}^{\circ }}\], which is,
We will now have to find the speed of the aeroplane in the given time, we will use the formula of speed, we get,
\[Speed=\dfrac{distance}{time}\]
 \[\Rightarrow Speed=\dfrac{\dfrac{5000}{\sqrt{3}}}{15}\]
\[\Rightarrow Speed=\dfrac{5000}{15\times 1.73}\]
As we know that, \[\sqrt{3}=1.73\].
We get,
\[\Rightarrow Speed=192.67m/s\]
Therefore, the speed of the aeroplane is \[192.67m/s\].

Note: The trigonometric functions used should be as per the values of the sides given. In the above solution, we were given the value of the base and we had to find the perpendicular, so we used tangent function, we could have also used cotangent function for the same, it’s as per our choice. Also, the correct values of the trigonometric function’s angles should be written, else the answer will get wrong. The diagram made should be as per what the question says and not adding or removing something extra of our own.