Question

Amit standing on a horizontal plane finds a bird flying at a distance of 200 meter from him at an angle of elevation ${30^0}$. Deepak standing on the roof of a 50 meter high building finds the angle of elevation of the same bird to be ${45^0}$. Amit and Deepak are on opposite sides of the bird. Find the distance of the bird from Deepak.

Answer 1

Hint – In this question let the Amit be standing at a point B, the bird flying at point C and Deepak standing at point G. Draw a perpendicular from the point C onto the line BD. Use the basic trigonometric ratios $\sin \theta $ preferred in respective triangles to get the value of CG.

Complete step-by-step solution -

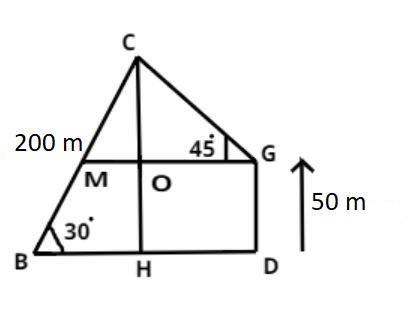
The bird is flying at point C and the position of Amit is at point B.
So according to question
$BC = 200$ meter and $\angle CBD = {30^0}$.
Now let us suppose GD is a 50 m high building.
And Deepak is standing at point G according to the question and Amit and Deepak are opposite to each other.
Now it is given that the angle of elevation of the bird from the Deepak is 45 degree.
$ \Rightarrow \angle CGM = {45^0}$
Now draw the perpendicular CH on line BD.
So in triangle BCH we know that Sin is the ratio of perpendicular to hypotenuse.
$ \Rightarrow \sin {30^0} = \dfrac{{CH}}{{BC}} = \dfrac{{CH}}{{200}}$
Now as we know that sin 30o = (1/2) therefore
$ \Rightarrow CH = \dfrac{{200}}{2} = 100$ meter.
Now by symmetry the length of OH = GD = 50.
Therefore from figure
CH = CO + OH
$ \Rightarrow 100 = CO + 50$
$ \Rightarrow CO = 100 - 50 = 50$ meter.
Now in triangle COG
$ \Rightarrow \sin {45^0} = \dfrac{{CO}}{{CG}} = \dfrac{{50}}{{CG}}$
$ \Rightarrow CG = \dfrac{{50}}{{\sin {{45}^0}}} = \dfrac{{50}}{{\dfrac{1}{{\sqrt 2 }}}} = 50\sqrt 2 = 70.71$ meter. $\left[ {\because \sin {{45}^0} = \dfrac{1}{{\sqrt 2 }},\sqrt 2 = 1.414} \right]$
So the distance between the Deepak and the bird is 42.42 meter.
So this is the required answer.

Note – In these types of questions it is always advisable to draw the diagrammatic representation using the information provided in the question as it helps understanding the geometry of the figure involved. Basic understanding of symmetric length like OH = GD in this case, helps getting to answer.