
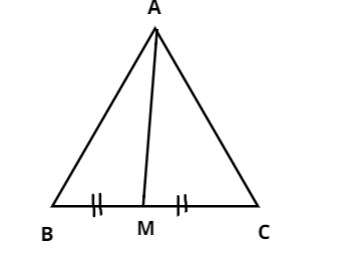
AM is a median of a triangle ABC. Is $AB + BC + CA > 2AM$. (Consider the sides of the triangle $\Delta ABM$ and $\Delta AMC$)

Answer
605.4k+ views
Hint: Here, we will use the property of triangle i.e.., the sum of lengths of any two sides in a triangle should be greater than the length of the third side to prove the given condition $AB + BC + CA > 2AM$.
Complete step-by-step answer:
Given,
AM is a median of a triangle ABC and the triangle is divided into$\Delta ABM{\text{ }}$and $\Delta AMC$.
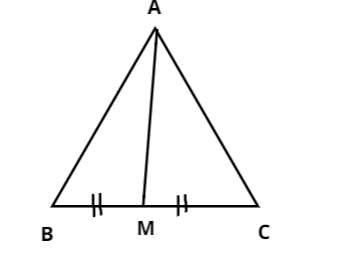
As we know the property of a triangle i.e.., the sum of lengths of any two sides in a triangle should be greater than the length of the third side. Therefore, let us consider the triangle ABM, we get
$AB + BM > AM \to (i)$
Similarly, from$\Delta AMC$, we get
$AC + MC > AM \to (ii)$
Let us add equation (i) and (ii), we get
$\Rightarrow AB + BM + AC + MC > AM + AM \\$
$\Rightarrow AB + AC + (BM + MC) > 2AM \to (iii) \\ $
From the $\Delta ABC$, we know that
$\Rightarrow$ $BM + MC = BC \to (iv)$
So, let us substitute the equation (iv) in equation (iii), we get
$\Rightarrow$ $AB + BC + CA > 2AM$
Hence, equation (i) is proved.
Note: A median of a triangle is a line segment that joins a vertex to the midpoint of the side that is opposite to the vertex bisecting into two equal parts. Here, $BM = MC$ and the area of the triangles ABM and AMC are equal.
Complete step-by-step answer:
Given,
AM is a median of a triangle ABC and the triangle is divided into$\Delta ABM{\text{ }}$and $\Delta AMC$.

As we know the property of a triangle i.e.., the sum of lengths of any two sides in a triangle should be greater than the length of the third side. Therefore, let us consider the triangle ABM, we get
$AB + BM > AM \to (i)$
Similarly, from$\Delta AMC$, we get
$AC + MC > AM \to (ii)$
Let us add equation (i) and (ii), we get
$\Rightarrow AB + BM + AC + MC > AM + AM \\$
$\Rightarrow AB + AC + (BM + MC) > 2AM \to (iii) \\ $
From the $\Delta ABC$, we know that
$\Rightarrow$ $BM + MC = BC \to (iv)$
So, let us substitute the equation (iv) in equation (iii), we get
$\Rightarrow$ $AB + BC + CA > 2AM$
Hence, equation (i) is proved.
Note: A median of a triangle is a line segment that joins a vertex to the midpoint of the side that is opposite to the vertex bisecting into two equal parts. Here, $BM = MC$ and the area of the triangles ABM and AMC are equal.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Which of the following does not have a fundamental class 10 physics CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




