Question

Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” (Isn’t this interesting) Represent this situation algebraically and graphically.

Answer 1

Hint- Here, we will be proceeding by assuming the present ages of Aftab and his daughter as two different variables and then forming two equations in two variables according to the problem statement.

Let us suppose that the present age of Aftab be $x$ years and the present age of Aftab’s daughter be $y$ years.
According to problem statement seven years ago, Aftab was seven times older than Aftab’s daughter i.e., $x - 7 = 7\left( {y - 7} \right) \Rightarrow x - 7 = 7y - 49 \Rightarrow x - 7y = - 42{\text{ }} \to (1)$
Also three years later, Aftab will be three times as old as Aftab’s daughter at that time i.e., $x + 3 = 3\left( {y + 3} \right) \Rightarrow x + 3 = 3y + 9 \Rightarrow x - 3y = 6{\text{ }} \to {\text{(2)}}$
As we know that the general equation of any straight line having slope $m$ and y-intercept as $c$ is given by $y = mx + c$
Equation (1) can be written as $ \Rightarrow x - 7y = - 42 \Rightarrow 7y = x + 42 \Rightarrow y = \dfrac{x}{7} + 6{\text{ }} \to {\text{(3)}}$
and equation (2) can be written as $ \Rightarrow x - 3y = 6 \Rightarrow 3y = x - 6 \Rightarrow y = \dfrac{x}{3} - 2{\text{ }} \to {\text{(4)}}$
Both the equations (1) and (2) represent equations in two variables.
Clearly, we can see that equation (3) represents the equation of a straight line having slope $\dfrac{1}{7}$ and y-intercept as 6.
Equation (4) also represents the equation of a straight line having slope $\dfrac{1}{3}$ and y-intercept as $\left( { - 2} \right)$.
For a point where these two straight lines cut each other or for the solution of these two straight lines.
Subtracting equation (1) from equation (2), we get
$ \Rightarrow x - 3y - x + 7y = 6 + 42 \Rightarrow 4y = 48 \Rightarrow y = 12$
Put the above value of $y$ in equation (1), we get
$ \Rightarrow x - 7\left( {12} \right) = - 42 \Rightarrow x = - 42 + 84 \Rightarrow x = 42$
Hence, the present age of Aftab is 42 years and the present age of his daughter is 12 years.
Therefore, the straight lines given by equations (3) and (4) or by equations (1) and (2) meet at a point having coordinates $\left[ {42,12} \right]$.
The above solution represents the situation algebraically.
In order to obtain the graphical solution to the given situation, we will put y=0 in equations (1) and (2) and this will give us a passing point apart from the other passing point i.e., $\left[ {42,12} \right]$
Equation (1) becomes
$ \Rightarrow x - \left( {7 \times 0} \right) = - 42 \Rightarrow x = - 42$
Hence, the straight line represented by equation (1) passes through two points which are (-42,0) and (42,12)
Equation (2) becomes
$ \Rightarrow x - \left( {3 \times 0} \right) = 6 \Rightarrow x = 6$
Hence, the straight line represented by equation (2) passes through two points which are (6,0) and (42,12)
The graphical solution to this problem is shown in the figure.

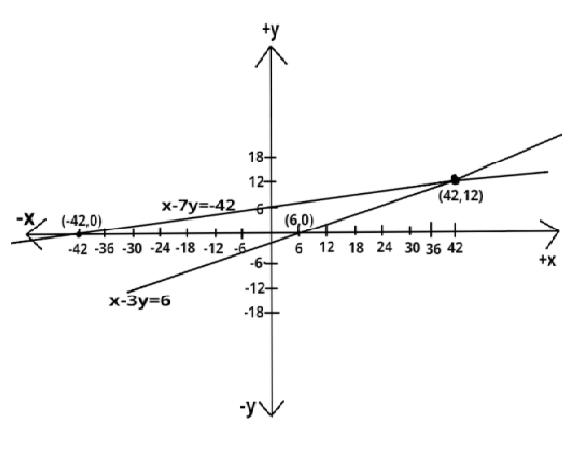
Note- In these types of problems, we represent the problem statement in terms of two equations with two variables and then compare these equations with the general form of straight lines. Here, we find the point of intersection of these two straight lines. Both of these straight lines pass through this point because these two meet at this particular point.