Question

$ABCDEF$ is a regular hexagon in the $XY$ plane vertices in the anti-clockwise sense. \[\overrightarrow {AB} = 2\hat i\], then $\overrightarrow {CD} = $
A) \[\hat i - \sqrt 3 \hat j\]
B) $\hat i + \sqrt 3 \hat j$
C) $ - \hat i + \sqrt 3 \hat j$
D) $ - \hat i - \sqrt 3 \hat j$

Answer 1

Hint: Here, it is given that $ABCDEF$ is a regular hexagon means all the sides are of equal length of \[2\] units and is in the $XY$ plane. We can assume that the vertex $A$ of the regular hexagon is the origin of the coordinate system and then we can find the coordinate of all other vertices by using some trigonometric equations. Then to find the vector equation of any sides we can simply subtract both the coordinates of two vertices and put $\hat i$ with $x$ coordinates and $\hat j$ with $y$ coordinate.

Complete step-by-step solution:
Here, it is given that $ABCDEF$ is a regular hexagon in the $XY$ plane vertices in the anti-clockwise sense. And we have to find $\overrightarrow {CD} = $
 

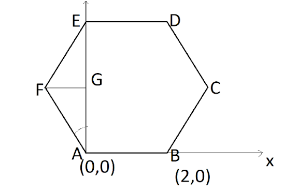
Let vertex $A$ be the origin of the coordinate system and vertex $B$ lie on the $x$ axis two units away from the origin. So, the coordinate of $A$ is $\left( {0,0} \right)$ and the coordinate of $B = \left( {2,0} \right)$.
Now, $AFG$ is a triangle in which $\angle FAG = 3{0^ \circ }$ as $\angle FAG = \angle FAB - \angle G{\rm A}{\rm B}$ and each angle of hexagon is $\angle FAB = 12{0^ \circ }$ and $\angle GAB = {90^ \circ }$ because both axis are perpendicular to each other.
Side $AG = AF\cos {30^ \circ }$
Putting the length of side $AF$ and value of $\cos {30^ \circ }$ we get,
$AG = 2 \times \dfrac{{\sqrt 3 }}{2} = \sqrt 3 $
And the side $FG = AF\sin {30^ \circ }$
Putting the length of side $AF$ and value of $\sin {30^ \circ }$ we get,
$FG = 2 \times \dfrac{1}{2} = 1$
Now, the coordinate of vertex $C = \left( {2 + 1,\sqrt 3 } \right) = \left( {3,\sqrt 3 } \right)$. And vertex $D = \left( {2,2\sqrt 3 } \right)$, vertex ${\rm E} = \left( {0,2\sqrt 3 } \right)$ and vertex $F = \left( { - 1,\sqrt 3 } \right)$.
Now, we have two find the vector $\overrightarrow {CD} $ and we get this by subtracting the coordinates of vertex $C$ from the coordinates of vertex $D$. So,
$
  \overrightarrow {CD} = \left( {2 - 3} \right)\hat i + \left( {2\sqrt 3 - \sqrt 3 } \right)\hat j \\
  \overrightarrow {CD} = - \hat i + \sqrt 3 \hat j
 $

Thus, option (C) is correct.

Note: Similarly, other sides vectors like $\overrightarrow {BC} ,\overrightarrow {DE} ,\overrightarrow {EF} $ and $\overrightarrow {FA} $ can be found by subtracting the coordinates of two vertices. Only care while subtracting the coordinates should be taken is subtract the coordinates of the first vertex from that of the second vertex. And put $\hat i$ corresponding to $x$ coordinates and $\hat j$ corresponding to $y$ coordinates.