Question

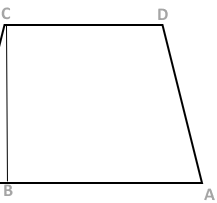
ABCD is a trapezium such that AB is parallel to CD and CB is perpendicular to them. If $\angle ADB = \theta $, BC=p and CD=q, show that: $AB = \dfrac{{({p^2} + {q^2})\sin \theta }}{{p\cos \theta + q\sin \theta }}$

Answer 1

Hint: $\vartriangle BCD$ is a right-angled triangle so we can use Pythagoras theorem. Also the sum of all the angles of the triangle is $\pi $.

From the right-angle triangle $\vartriangle BCD$, we get, $BD = \sqrt {{p^2} + {q^2}} $ . Let $\angle ADB = \angle BDC = \alpha $ then $\angle DAB = \pi - (\alpha - \theta )$ and $\tan \alpha = \dfrac{p}{q}$. Now, from $\vartriangle ABD$, we have
$
  \dfrac{{AB}}{{\sin \theta }} = \dfrac{{BD}}{{\sin [\pi - (\theta + \alpha )]}} = \dfrac{{BD}}{{\sin (\theta + \alpha )}} \\
  \therefore AB = \dfrac{{BD\sin \theta }}{{\sin (\theta + \alpha )}} = \dfrac{{B{D^2}\sin \theta }}{{BD\sin (\theta + \alpha )}} \\
   = \dfrac{{B{D^2}\sin \theta }}{{BD\sin \theta \cos \alpha + BD\cos \theta \sin \alpha }} \\
   = \dfrac{{({p^2} + {q^2})\sin \theta }}{{q\sin \theta + p\cos \theta }} \\
$
Hence proved.

Note: Proving questions are likely to be moderate in comparison to other questions. We need to have an idea or a path we can say to reach the goal.