Question

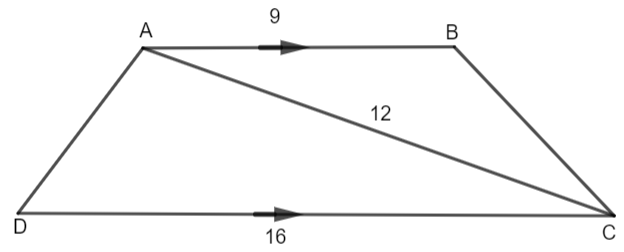
ABCD is a trapezium, AB||CD, AB = 9, AC = 12 and CD = 16.
(i) Prove that \[\Delta ABC\sim \Delta CAD.\]
(ii) If AD = 10, find BC.

Answer 1

Hint: To solve the given question, we will first find out what a trapezium is. Then, to prove the two given triangles as similar, we will prove that the ratio of two corresponding sides are the same and the angle included between these sides in both the triangles are the same. Thus, they will be similar by the SAS criterion. To solve the second part, we will find the length of BC by making use of the fact that in two similar triangles, the ratio of corresponding sides remains the same.

Complete step by step solution:
Before we solve the given question, we must know that a trapezium is a polygon in which one pair of the opposite sides are parallel and the other pair is non-parallel. Now, we will solve both parts separately.
(i) In this part, we have to prove that triangles ABC and CAD are similar. Any two given triangles are said to be similar if the ratio of the corresponding sides of both triangles is the same or the corresponding angles are the same. Now, we will consider triangles ABC and CAD.

From the above triangles, we can say that,
\[\dfrac{AB}{CA}=\dfrac{9}{12}=\dfrac{3}{4}.......\left( i \right)\]
Similarly,
\[\dfrac{AC}{CD}=\dfrac{12}{16}=\dfrac{3}{4}.......\left( ii \right)\]
Thus from (i) and (ii), we will get,
\[\dfrac{AB}{CA}=\dfrac{AC}{CD}.......\left( iii \right)\]
Now, \[\angle BAC=\alpha \] and \[\angle ACD=\beta .\] Now it is given in the question that AB||CD. Now, AB and CD are parallel and the diagonal AC acts as a transversal, so \[\angle BAC\] and \[\angle ACD\] will be the same because they are a pair of alternate interior angles. Thus, we have,
\[\angle BAC=\angle ACD\]
\[\Rightarrow \alpha =\beta ......\left( iv \right)\]
From (iii) and (iv), we can say that two corresponding sides of both the triangles are in the same ratio and the included angle between these sides in both triangles is the same. Thus, these triangles will be similar according to the side – angle – side (SAS) criterion. Thus,
\[\Delta ABC\sim \Delta CAD\]
Hence proved.
(ii) Now, we know that in both the triangles, the side ratio will remain the same, i.e.
\[\dfrac{AB}{CA}=\dfrac{AC}{CD}=\dfrac{BC}{AD}\]
\[\Rightarrow \dfrac{3}{4}=\dfrac{3}{4}=\dfrac{BC}{AD}\]
\[\Rightarrow BC=\dfrac{3}{4}\left( AD \right)\]
Now, AD = 10, so we will get,
\[\Rightarrow BC=\dfrac{3}{4}\times 10\]
\[\Rightarrow BC=\dfrac{15}{2}\]
\[\Rightarrow BC=7.5\]

Note: The order in which we write the vertices of the triangle in \[\Delta ABC\sim \Delta CAD\] is important. We can say that \[\Delta ABC\sim \Delta CAD\] is not the same as \[\Delta ACB\sim \Delta CAD.\] \[\Delta ACB\sim \Delta CAD\] means \[\dfrac{AC}{CA}=\dfrac{CB}{AD}=\dfrac{AB}{CD}\] and \[\angle A=\angle C,\angle C=\angle A,\angle B=\angle D\] whereas \[\Delta ABC\sim \Delta CAD\] means that \[\dfrac{AB}{CA}=\dfrac{BC}{AD}=\dfrac{AC}{CD}\] and \[\angle A=\angle C,\angle B=\angle A,\angle C=\angle D.\] Thus, they are not the same and we should be careful while writing these.