Question

ABCD is a rectangle with sides 36cm and 90cm. P is a point on BC which is one of the longer sides such that PA=2PD. The length of PB is
A) 80 cm
B) 76 cm
C) 72 cm
D) 64 cm

Answer 1

Hint:
First draw a suitable diagram of the rectangle. Then, take a pint on BC. Take both right angled triangles and apply Pythagoras theorems. Compare both expressions together as $PA= 2 PD$. Solve the quadratic equation, thus obtained. Suitable root of it will be the result.

Complete step by step solution:
Draw the rectangle ABCD as below.

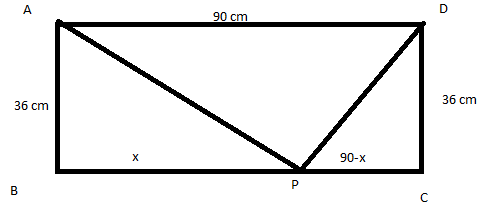
Sides AB and DC are equal and 36 cm.
Also, sided AC and AD are 90 cm.
Let us assume that P is appointed somewhere on side BC.
It is given that ,
PA = 2 PD …(1)
Now let us assume that length of BP is x cm,
So, the PC will be (90-x) cm.
In right angled triangle ABP, we apply the Pythagoras theorem, and hence we get,
$P{A^2} = A{B^2} + B{P^2}$
Substituting the values in above equation, we have
$P{A^2} = {36^2} + {x^2}$ …(2)
Similarly in right angled triangle CPD, we apply the Pythagoras theorem, and hence we get,
$P{D^2} = P{C^2} + D{C^2}$
Substituting the values in above equation, we have
$P{D^2} = {36^2} + {(90 - x)^2}$ …(3)
Doing square on both sides of equation (1), we get
$P{A^2} = 4P{D^2}$
Now, from equations (2) and (3) in the above equation, we have
${36^2} + {x^2} = 4({36^2} + {(90 - x)^2})$
Further simplification, we get
$
  {36^2} + {x^2} = 4({36^2} + {(90 - x)^2}) \\
   \Rightarrow {36^2} + {x^2} = 4 \times {36^2} + 4 \times {(90 - x)^2} \\
   \Rightarrow {x^2} = 3 \times {36^2} + 4 \times (8100 + {x^2} - 180x) \\
   \Rightarrow {x^2} = 3888 + 32400 + 4{x^2} - 720x \\
   \Rightarrow 3{x^2} - 720x + 36288 = 0 \\
   \Rightarrow {x^2} - 240x + 12096 = 0 \\
 $
Thus we have a quadratic equation. Two factors of 12096 are 168 and 72. Thus doing factorization of above equation we get,
$(x-168) (x-72) = 0$
Thus values of $x = 168$ and $72$.
Since $168 > 90$, which is not possible for point P.
Thus a suitable value of $x = 72$.
$\therefore $ The length of PB will be 72 cm.

So, the correct option is C.

Note:
This question is a direct application of Pythagoras theorem. Also, solving the quadratic equation is an important part of such problems. In this way, we can solve a geometrical problem with the help of algebraic computations.