Question

ABCD is a rectangle in which diagonal AC bisects $\angle $${\text{A}}$ as well as $\angle $${\text{C}}$.
Show that,
(i) ABCD is square
(ii) diagonal BD bisects $\angle $${\text{B}}$ as well as $\angle $${\text{D}}$.

Answer 1

Hint: To solve this question we need to know the basic theory related to the rectangle. We learned that a rectangle has four-sided and all the internal angles are equal to 90 degrees. The length of the opposite sides of the rectangle is always equal to each other. The length of the opposite sides of the rectangle is always equal to each other. If all the sides are equal then it is square.

Complete step-by-step solution:
(i) we need to prove ABCD is square.
Given in question,
ABCD is a rectangle, in which diagonal AC bisect $\angle $${\text{A}}$ as well as $\angle $${\text{C}}$.
        

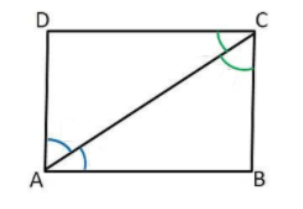
Therefore,
$\angle $${\text{DAC}}$=$\angle $${\text{CAB}}$……………… (1)
$\angle $${\text{DCA}}$=$\angle $${\text{BCA}}$………………. (2)
A square is a rectangle when all sides are equal. Now,
AD$\parallel $BC & AC is transversal, therefore
$\angle$${\text{DAC}}$=$\angle$${\text{BCA}}$ [Alternate angles]
From (1),
$\angle $${\text{CAB}}$=$\angle $${\text{BCA}}$……………….. (3)
In $\vartriangle $ABC,
$\angle $${\text{CAB}}$=$\angle $${\text{BCA}}$, therefore
BC=AB………………….. (4) [sides opposite to equal angles]
But BC=AD & AB=DC………………….. (5) [Opposite sides of rectangle]
Therefore from (4) & (5),
AB=BC=CD=AD
Hence, ABCD is a square.
(ii) we need to prove that diagonal BD bisects $\angle $${\text{B}}$ as well as $\angle $${\text{D}}$.
Now, As we discussed in the previous part.
ABCD is a square and we know that diagonals of a square bisect its angles.
Hence, BD bisects ∠B as well as ∠D.

Note: Here we use various properties of a rectangle. Always remember that the diagonals of a rectangle bisect each other and also the sides in a rectangle are always equal to each other.