Question

$ABCD$ is a rectangle in which diagonal $AC$ bisects $\angle A$ as well as $\angle C$. Which of the following statements is/are true:
(i) $ABCD$ is a square
(ii) diagonal $BD$ bisects $\angle B$as well as $\angle D$
A) (i) only
B) (ii) only
C) (i) and (ii) both
D) None of these

Answer 1

Hint:By using the properties of a rectangle and the statement that the diagonal $AC$ bisects $\angle A$ as well as $\angle C$. We need to find out whether given two statements are true or false.

Complete step-by-step answer:
Now $ABCD$ is a rectangle whose diagonal $AC$ bisects $\angle A$ as well as $\angle C$.

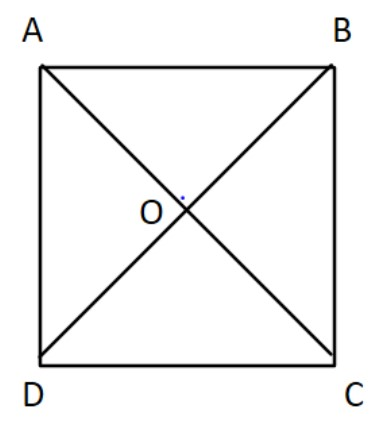
This means
$AB = CD\,\,\,\,\& \,\,\,AD = BC$
[As opposite sides of rectangle are equal]
$\angle A = \angle B = \angle C = \angle D = {90^ \circ }$
[As all the angles of rectangles are right angles]
$\angle ACD = \angle ACB\,\,\,\,\& \,\,\,\,\,\angle CAD = \angle CAB\,\,\,\,\,\,\,\,\,\,\,\,\,\, \to (1)$
[As $AC$ bisects $\angle A$ as well as $\angle C$]
Now we need to check whether $ABCD$ is a square or not.
For that we just need to prove that the adjacent sides of the rectangle are equal.
Since $ABCD$ is a rectangle, its opposite sides are parallel which means $AB\left\| {CD} \right.$
With $AB\left\| {CD} \right.$ and transverse
$\angle CAB = \angle DCA\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \to (2)$[Alternate interior angles]
From equations (1) and (2) we get
$\angle CAD = \angle DCA\,$
Since sides opposite to equal angles are also equal
Therefore, $DC = AD$
As opposite sides of a rectangle are equal
$ \Rightarrow AB = BC = CD = DA\,\,\,\, \to (3)$
Hence $ABCD$ is a square
Now in order to check whether diagonal $BD$ bisects $\angle B$ as well as $\angle D$. We need to prove $\angle DBA = \angle DBC\,\,\,\& \,\,\angle CDB = \angle ADB$
In $\Delta BDA\,\,\& \,\,\Delta DBC$
$BD = DB\,$ [common]
$DA = BC\,$[proved above in equation (3)]
$BA = DC\,$[proved above in equation (1)]
Hence by using SSS congruence rule i.e. the corresponding sides are equal to each other
$\Delta BDA \cong \Delta DBC$
Since corresponding parts of congruent triangles are equal
Therefore, $\angle ABD = \angle CDB\,\,\,\,\,\,\,\, \to (4)$
Now $BC = AD\,$[sides of a square]
$ \Rightarrow \angle CDB = \angle CBD\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \to (5)$[opposite angles of equal sides are equal]
Hence by using (4) and (5) we get
$\angle ABD = \angle CBD$
So $BD$ bisects $\angle B$
Similarly $\angle BDA = \angle DBC\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \to (6)$[CPCT]
Also $\angle BDC = \angle DBC\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \to (7)\,$[$BC = CD$]
So from (6) and (7) we get
$\angle BDC = \angle BDA$
Hence $BD$ bisects $\angle D$
Therefore both equations (i) and (ii) are true.

So, the correct answer is “Option C”.

Note:in such questions we need to remember all the properties that the figure has. A property we did not use in this question was diagonals of a rectangle bisect each other. It may not have been used now but can be used in other questions. Hence we need to remember all the properties.