Questions & Answers
Question
Answers
Related Questions
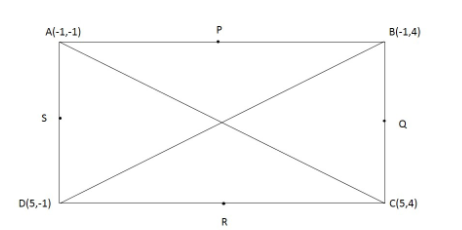
ABCD is a rectangle formed by the points \[{\text{A}}( - 1,\; - 1)\] , \[{\text{B}}( - 1,\;4)\], C(5, 4) and \[{\text{D}}(5,\; - 1)\]. P, Q, R, S are the mid point of AB, BC, CD, DA. Is the Quadrilateral a square? A rectangle? Or a rhombus? Justify your answer.
Answer
![Verified]()
Verified
Verified
Hint: Here, in this problem, we will use the midpoint formula to find the midpoints of the sides of the rectangle ABCD and then will find its diagonal to see whether it's rhombus or square.
Complete step-by-step answer:
\[\begin{align}
& \text{For QR; Here, }{{x}_{1}}=2\ ;\ {{y}_{1}}\ =\ 4 \\
& \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{x}_{2}}\ =\ 5\ ;\ {{y}_{2}}\ =\ 3\text{/}2 \\
\end{align}\]
Using distance formula
\[\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
\[\text{QR}\ \text{=}\ \sqrt{{{(5-2)}^{2}}\ +\ {{\left( \dfrac{3}{2}-4 \right)}^{2}}}\]
\[=\sqrt{{{(3)}^{2}}+{{\left( \dfrac{3-8}{2} \right)}^{2}}}\]
\[=\sqrt{9+{{\left( \dfrac{-5}{2} \right)}^{2}}}\]
\[=\sqrt{9+\dfrac{25}{4}}=\sqrt{\dfrac{36+25}{4}}=\sqrt{\dfrac{61}{4}}\ \text{units}\text{.}\]
\[\begin{align}
& \text{For RS}\ \text{; Here, }{{x}_{1}}=5\ ;\ {{y}_{1}}\ =\ 3\text{/}2 \\
& \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{x}_{2}}\ =\ 2\ ;\ {{y}_{2}}\ =\ -1 \\
\end{align}\]
\[\text{RS = }\sqrt{{{(2-5)}^{2}}+{{(-1-3\text{/}2)}^{2}}}\]
\[=\sqrt{{{(-3)}^{2}}+{{\left( \dfrac{-2-3}{2} \right)}^{2}}}=\sqrt{9+{{\left( \dfrac{-5}{2} \right)}^{2}}}=\sqrt{9+\dfrac{25}{4}}\]
\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\sqrt{\dfrac{36+25}{4}}=\sqrt{\dfrac{61}{4}}\ \text{units}\text{.}\]
\[\begin{align}
& \text{For SP}\ \text{; Here, }{{x}_{1}}=2\ ;\ {{y}_{1}}\ =\ -1 \\
& \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{x}_{2}}\ =\ -1\ ;\ {{y}_{2}}\ =\ 3\text{/}2 \\
\end{align}\]
\[\text{SP}\ \text{=}\ \sqrt{{{(-1-2)}^{2}}+{{\left( \dfrac{3}{2}+1 \right)}^{2}}}\]
\[=\sqrt{{{(-3)}^{2}}+{{\left( \dfrac{3+2}{2} \right)}^{2}}}\]
\[=\sqrt{9+\dfrac{25}{4}}\]
\[=\sqrt{\dfrac{36+25}{4}}\]
\[=\sqrt{\dfrac{61}{4}}\ \text{units}\text{.}\]
Points S is the midpoint of AD. Applying midpoint formula:
Coordinates of S:-$\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2}-,\dfrac{{{y}_{1}}+{{y}_{2}}}{2}- \right)$
Here : ${{x}_{1}}=-1;\ {{y}_{1}}=-1$
${{x}_{2}}=5;\ {{y}_{2}}=-1$
Coordinates of $S=\left( \dfrac{-1+5}{2},\dfrac{-1-1}{2} \right)=\left( \dfrac{4}{2},\dfrac{-2}{2} \right)=\left( 2,-1 \right)$
Thus,
Vertices of quadrilateral PQRS are,
$P\left( \text{-1,}{\scriptstyle{}^{3}/{}_{2}} \right),Q\left( 2,4 \right),R\left( 5,{\scriptstyle{}^{3}/{}_{2}} \right)$ and $S\left( 2,-1 \right)$
Now, finding the sides of quadrilateral PQRS.
Applying distance formula;
\[\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
For PQ; Here, ${{x}_{1}}=-1;\ {{y}_{1}}={\scriptstyle{}^{3}/{}_{2}}$
${{x}_{2}}=2;\ {{y}_{2}}=4$
PQ $=\sqrt{{{\left( 2-\left( -1 \right) \right)}^{2}}+{{\left( 4-{\scriptstyle{}^{3}/{}_{2}} \right)}^{2}}}$
$=\sqrt{{{\left( 2+1 \right)}^{2}}+{{\left( \dfrac{8-3}{2} \right)}^{2}}}$
$=\sqrt{{{\left( 3 \right)}^{2}}+{{\left( \dfrac{5}{2} \right)}^{2}}}$
$=\sqrt{9+\dfrac{25}{4}}$
$=\sqrt{\dfrac{36+25}{4}}$
$=\sqrt{\dfrac{61}{4}}$ units.
Thus,
PQ = QR = RS = SP = $\sqrt{\dfrac{61}{4}}$ units.
$\therefore $ PQRS is a square, on a rhombus.
Now to check whether. PQRS is a square or a rhombus, we find the length of diagonals RP and SQ;
For RP:-${{x}_{1}}=-1;\ {{y}_{1}}={\scriptstyle{}^{3}/{}_{2}}$
${{x}_{2}}=5;\ {{y}_{2}}={\scriptstyle{}^{3}/{}_{2}}$
RP$=\sqrt{{{\left( 5+1 \right)}^{2}}+{{\left( \dfrac{3}{2}-\dfrac{3}{2} \right)}^{2}}}$
$=\sqrt{{{\left( 6 \right)}^{2}}+{{\left( 0 \right)}^{2}}}$
$\sqrt{{{6}^{2}}+0}$
6 units.
For SQ;$-{{x}_{1}}=2$ $;{{y}_{1}}=-1$
${{x}_{2}}=2$ $;{{y}_{2}}=4$
SQ$=\sqrt{{{\left( 2-2 \right)}^{2}}+{{\left( 4+1 \right)}^{2}}}$
$=\sqrt{{{\left( 0 \right)}^{2}}+{{\left( 5 \right)}^{2}}}$
$=\sqrt{{{\left( 5 \right)}^{2}}}=5$ units
Since RP $\ne $ SQ
$\therefore $ Diagonal of the quadrilateral are not equal.
So, PQRS is not a square.
$\therefore $ PQRS is Rhombus.
Note: In this type of problems, where we are asked to find whether the given point is a rectangle that will form a rhombus or a square, we have to use the midpoint formula and the distance formula to know the length of the sides and recognize the figure formed.
Complete step-by-step answer:
\[\begin{align}
& \text{For QR; Here, }{{x}_{1}}=2\ ;\ {{y}_{1}}\ =\ 4 \\
& \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{x}_{2}}\ =\ 5\ ;\ {{y}_{2}}\ =\ 3\text{/}2 \\
\end{align}\]
Using distance formula
\[\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
\[\text{QR}\ \text{=}\ \sqrt{{{(5-2)}^{2}}\ +\ {{\left( \dfrac{3}{2}-4 \right)}^{2}}}\]
\[=\sqrt{{{(3)}^{2}}+{{\left( \dfrac{3-8}{2} \right)}^{2}}}\]
\[=\sqrt{9+{{\left( \dfrac{-5}{2} \right)}^{2}}}\]
\[=\sqrt{9+\dfrac{25}{4}}=\sqrt{\dfrac{36+25}{4}}=\sqrt{\dfrac{61}{4}}\ \text{units}\text{.}\]
\[\begin{align}
& \text{For RS}\ \text{; Here, }{{x}_{1}}=5\ ;\ {{y}_{1}}\ =\ 3\text{/}2 \\
& \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{x}_{2}}\ =\ 2\ ;\ {{y}_{2}}\ =\ -1 \\
\end{align}\]
\[\text{RS = }\sqrt{{{(2-5)}^{2}}+{{(-1-3\text{/}2)}^{2}}}\]
\[=\sqrt{{{(-3)}^{2}}+{{\left( \dfrac{-2-3}{2} \right)}^{2}}}=\sqrt{9+{{\left( \dfrac{-5}{2} \right)}^{2}}}=\sqrt{9+\dfrac{25}{4}}\]
\[\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\sqrt{\dfrac{36+25}{4}}=\sqrt{\dfrac{61}{4}}\ \text{units}\text{.}\]
\[\begin{align}
& \text{For SP}\ \text{; Here, }{{x}_{1}}=2\ ;\ {{y}_{1}}\ =\ -1 \\
& \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{x}_{2}}\ =\ -1\ ;\ {{y}_{2}}\ =\ 3\text{/}2 \\
\end{align}\]
\[\text{SP}\ \text{=}\ \sqrt{{{(-1-2)}^{2}}+{{\left( \dfrac{3}{2}+1 \right)}^{2}}}\]
\[=\sqrt{{{(-3)}^{2}}+{{\left( \dfrac{3+2}{2} \right)}^{2}}}\]
\[=\sqrt{9+\dfrac{25}{4}}\]
\[=\sqrt{\dfrac{36+25}{4}}\]
\[=\sqrt{\dfrac{61}{4}}\ \text{units}\text{.}\]
Points S is the midpoint of AD. Applying midpoint formula:
Coordinates of S:-$\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2}-,\dfrac{{{y}_{1}}+{{y}_{2}}}{2}- \right)$
Here : ${{x}_{1}}=-1;\ {{y}_{1}}=-1$
${{x}_{2}}=5;\ {{y}_{2}}=-1$
Coordinates of $S=\left( \dfrac{-1+5}{2},\dfrac{-1-1}{2} \right)=\left( \dfrac{4}{2},\dfrac{-2}{2} \right)=\left( 2,-1 \right)$
Thus,
Vertices of quadrilateral PQRS are,
$P\left( \text{-1,}{\scriptstyle{}^{3}/{}_{2}} \right),Q\left( 2,4 \right),R\left( 5,{\scriptstyle{}^{3}/{}_{2}} \right)$ and $S\left( 2,-1 \right)$
Now, finding the sides of quadrilateral PQRS.
Applying distance formula;
\[\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
For PQ; Here, ${{x}_{1}}=-1;\ {{y}_{1}}={\scriptstyle{}^{3}/{}_{2}}$
${{x}_{2}}=2;\ {{y}_{2}}=4$
PQ $=\sqrt{{{\left( 2-\left( -1 \right) \right)}^{2}}+{{\left( 4-{\scriptstyle{}^{3}/{}_{2}} \right)}^{2}}}$
$=\sqrt{{{\left( 2+1 \right)}^{2}}+{{\left( \dfrac{8-3}{2} \right)}^{2}}}$
$=\sqrt{{{\left( 3 \right)}^{2}}+{{\left( \dfrac{5}{2} \right)}^{2}}}$
$=\sqrt{9+\dfrac{25}{4}}$
$=\sqrt{\dfrac{36+25}{4}}$
$=\sqrt{\dfrac{61}{4}}$ units.
Thus,
PQ = QR = RS = SP = $\sqrt{\dfrac{61}{4}}$ units.
$\therefore $ PQRS is a square, on a rhombus.
Now to check whether. PQRS is a square or a rhombus, we find the length of diagonals RP and SQ;
For RP:-${{x}_{1}}=-1;\ {{y}_{1}}={\scriptstyle{}^{3}/{}_{2}}$
${{x}_{2}}=5;\ {{y}_{2}}={\scriptstyle{}^{3}/{}_{2}}$
RP$=\sqrt{{{\left( 5+1 \right)}^{2}}+{{\left( \dfrac{3}{2}-\dfrac{3}{2} \right)}^{2}}}$
$=\sqrt{{{\left( 6 \right)}^{2}}+{{\left( 0 \right)}^{2}}}$
$\sqrt{{{6}^{2}}+0}$
6 units.
For SQ;$-{{x}_{1}}=2$ $;{{y}_{1}}=-1$
${{x}_{2}}=2$ $;{{y}_{2}}=4$
SQ$=\sqrt{{{\left( 2-2 \right)}^{2}}+{{\left( 4+1 \right)}^{2}}}$
$=\sqrt{{{\left( 0 \right)}^{2}}+{{\left( 5 \right)}^{2}}}$
$=\sqrt{{{\left( 5 \right)}^{2}}}=5$ units
Since RP $\ne $ SQ
$\therefore $ Diagonal of the quadrilateral are not equal.
So, PQRS is not a square.
$\therefore $ PQRS is Rhombus.
Note: In this type of problems, where we are asked to find whether the given point is a rectangle that will form a rhombus or a square, we have to use the midpoint formula and the distance formula to know the length of the sides and recognize the figure formed.
×
Sorry!, This page is not available for now to bookmark.
Like this
Liked
-
LIVECourses
-
Crash Courses 2021
-
Vedantu Pro
-
Vedantu Assist
-
Class 12
-
-
JEE
-
JEE Main & Advanced 2021
-
JEE Main & Advanced 2022
-
-
NEET
-
NEET 2021
-
NEET 2022
-
-
NDA
-
CBSE
-
Commerce
-
Class 11
-
Class 12
-
-
ICSE
-
Maharashtra Board
-
Class 9
-
Class 10
-
-
Micro Courses
-
-
FREEMaster Classes
-
PREMIUM1-on-1 Classes
-
Study Material
-
NCERT Solutions
-
Previous Year Papers
-
Mock Tests
-
Sample Papers
-
Reference Book Solutions
-
ICSE Solutions
-
School Syllabus
-
Revision Notes
-
Important Questions
-
Math Formula Sheets
-
-
More
Book your FREE Online counselling session
Share your contact information
Your FREE Online counselling session has been booked!
Vedantu academic counsellor will be calling you shortly for your Online Counselling session.
DONE
Please try again later
OK
NCERT Book Solutions
Reference Book Solutions
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
(Mon-Sun: 9am - 11pm IST)
Questions?
Chat with us
