Question

ABCD is a cyclic quadrilateral whose side AB is a diameter of the circle through A, B, C, D. If $\angle ADC = 130^\circ $ , find $\angle BAC$
(A) $40^\circ $
(B) $50^\circ $
(C) $60^\circ $
(D) $30^\circ $

Answer 1

Hint: Join point C and A, to get two triangles $\Delta ADC$ and $\Delta BAC$. Now use the property of cyclic quadrilateral to find the measure of angle $\angle CBA$ and use the property that a triangle with one of its arms as diameter of circle always makes a right angle at the circumference.

Complete step-by-step answer:

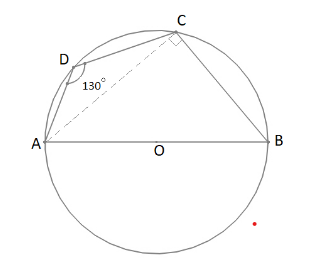
Given that the $\angle ADC = 130^\circ $ and ABCD is a cyclic quadrilateral, i.e. each pair of opposite angles of ABCD have sum equal to $180^\circ $.
Therefore $\angle CBA + \angle ADC = 180^\circ \Rightarrow \angle CBA = 180^\circ - 130^\circ = 50^\circ $
Let’s now join the points C and A to get triangle $\Delta ADC$ and $\Delta BAC$.
Now in $\Delta BAC$, we use the property which states that any triangle having diameter of a circle as its base will always subtend a right angle at the circumference, i.e. $\angle BCA = 90^\circ $
So, we have got $\angle BCA = 90^\circ $ and $\angle CBA = 50^\circ $ in $\Delta BAC$. Now we can easily calculate the third angle by the property that sum of all the interior angles of a triangle is $180^\circ $
$\angle BAC + \angle ACB + \angle CBA = 180^\circ $
Substituting all the known angles in the above relation, you get
$\angle BAC + 90^\circ + 50^\circ = 180^\circ $
$\angle BAC = 180^\circ - 140^\circ = 40^\circ $
Option A is the correct answer.

Note: Try to understand every detail mentioned in the question. Don’t assume anything until it's given. A cyclic quadrilateral is defined as a quadrilateral inscribed in a circle with all the points on the circumference. Cyclic quadrilateral can also be termed as inscribed quadrilateral. Getting handy with the properties of circles and quadrilaterals will always help you with these kinds of questions.