Question

ABCD is a cyclic quadrilateral .If AB∥CD, AD=5cm , then the length of BC is :
A $5\text{ }cm$
B $\text{6 }cm$
C $\text{7 }cm$
D $\text{8 }cm$

Answer 1

Hint:
Here we need to apply the concept of Cyclic Quadrilateral, Parallelogram, Transversal, isosceles triangle.
Cyclic Quadrilateral: A quadrilateral inscribed in a circle in which the sum of opposite angles is ${{180}^{\circ }}$ .
Quadrilateral: Four sided closed figure in which the sum of adjacent angles is ${{180}^{\circ }}$ .
Parallelogram: Four sided closed figure in which opposite sides are parallel and equal.
Isosceles triangle: Two angles are equal in a triangle it becomes isosceles triangle. Sides opposite to two equal angles are equal
Transversal: A line which cuts two or more parallel lines.

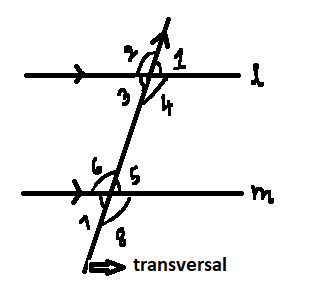
\[1=3\text{ },\text{ }5=7,\text{ }2=4\text{ }and\text{ }6=8\] :vertically opposite angles.
Sum of two adjacent angles is ${{180}^{\circ }}$
Sum of two co- interior angles is ${{180}^{\circ }}$i.e\[,\text{ }4+5,6+3\] .
Corresponding angles are equal, \[1=5,\text{ }2=6,3=7\text{ }and\text{ }4=8.\]
We need to find the length of BC.

Complete step by step solution:

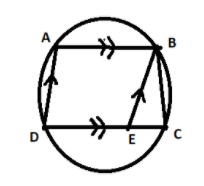
\[AD\] is transversal to \[AB\] and\[CD\] .
$\Rightarrow \angle A+\angle D={{180}^{\circ }}$ (Sum of two co- interior angles is${{180}^{\circ }}$)…………(1)
\[ABCD\] is a cyclic quadrilateral
\[\Rightarrow \angle A+\angle C={{180}^{\circ }}\]( Sum of two opposite angles is ${{180}^{\circ }}$)……………(2)
From the above equations 1 and 2,
\[\Rightarrow \angle A+\angle D=\angle A+\angle C\]
\[\therefore \angle C=\angle D\] …………………….(3)
Draw a line \[BE\] which is parallel to \[AD\], then it forms a \[\Delta BEC\]
\[DE\] becomes transversal to \[AD\] and \[BE\],
$\Rightarrow \angle BEC=\angle ADE$ ………….(4) (Corresponding angles are equal)
From equation 3 and 4 we can conclude that ,
\[\angle BEC=\angle ADE=\angle BCE\]
\[\therefore \angle BEC=\angle BCE\] ………….(5)
As two angles are equal in a triangle it becomes an isosceles triangle. Sides opposite to two equal angles are equal.
$\Rightarrow BC=BE$ …………….(6)
But \[ABED\] forms a parallelogram (Opposite sides are equal)

\[\Rightarrow =BE=\] ⇒ \[AD\]\[=B\text{ }E=\] \[5\text{ }cm\] ……………….(7)

From equations 6 and 7,

$\Rightarrow $ \[BC=BE=AD=\] \[5\text{ }cm\]

$\therefore $ \[BC\text{ }=\] \[5\text{ }cm\]

Therefore, the length of \[BC\text{ }=\]\[5\text{ }cm\].
Hence, Option choice A is the correct answer.

Note:
In such types of questions the concept of Cyclic Quadrilateral, Parallelogram, Transversal, isosceles triangle is needed. Knowledge about the concepts helps in applying the concept to the question. Then it is solved accordingly to get the required value.