Question

ABCD is a cyclic quadrilateral BA and CD produced, met at E. Prove that \[\vartriangle EBC\] and \[\vartriangle EBC\] are equiangular.

Answer 1

Hint: Draw a cyclic quadrilateral ABCD, name the angles as A, B, C, D according to the respective vertices with BA and CD produced, meeting at E. Then, according to the properties of cyclic quadrilaterals, $\angle A + \angle C = {180^ \circ },\angle B + \angle D = {180^ \circ }$ prove that the \[\vartriangle EBC\] and \[\vartriangle EBC\] are equiangular.

Complete step-by-step answer:
As given in the question that ABCD is a cyclic quadrilateral, so construct a cyclic quadrilateral ABCD and produce BA and CD which meets at E. So, the figure is shown below-

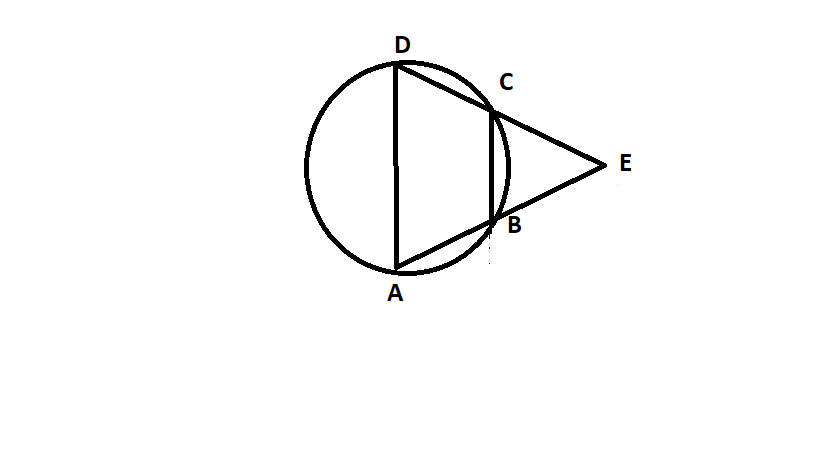
Now, in triangle EBC,
$\angle EBC + \angle B = {180^ \circ } \to (1)$ {Angles on a straight line}
Also, as we know that in a cyclic quadrilateral, $\angle A + \angle C = {180^ \circ },\angle B + \angle D = {180^ \circ }$.
Now using, $\angle D + \angle B = {180^ \circ } \to (2)$
Now, on subtracting equation (2) from equation (1), we get-
$
  \angle EBC + \angle B - \angle B - \angle D = {180^ \circ } - {180^ \circ } \\
   \Rightarrow \angle EBC = \angle D \to (3) \\
$
Similarly, by the angles on a straight-line property, we can say-
$\angle ECB + \angle C = {180^ \circ } \to (4)$
Also, we know- $\angle A + \angle C = {180^ \circ } \to (5)$
Similarly, we can say by subtracting equation (5) from equation (4), we get-
$
  \angle ECB + \angle C - \angle C - \angle A = {180^ \circ } - {180^ \circ } \\
   \Rightarrow \angle ECB = \angle A \to (6) \\
 $
Therefore, in triangle EDA, we have-
$\angle EAD = \angle A$
$\angle EDA = \angle D$ and $\angle DEA = \angle DEA$ (common angle).
This implies the \[\vartriangle EBC\] and \[\vartriangle EBC\] are equiangular.

Note: Whenever such types of questions appear, then make a rough sketch of the figure, then by using the properties of the cyclic quadrilateral, as mentioned in the solution, prove that the \[\vartriangle EBC\] and \[\vartriangle EBC\] are equiangular.