Question

A wire when bent in the form of a square encloses an area of $992.25\text{ c}{{\text{m}}^{2}}$ . If the same wire is bent in the form of a semicircle, what will be the radius of the semicircle so formed?

Answer 1

Hint: To find the radius of the semicircle formed from a wire that is used to make a square, we will find the side of the square using the given area and equation $\text{Area}={{a}^{2}}$ . Since the same wire is used to make a semicircle, we know that the perimeter of the square = circumference of the semicircle. Let us use the formula for circumference of semicircle, that is, $\pi r+2r$ and substitute this to the perimeter of the square to get the value of the radius.

Complete step by step answer:
We need to find the radius of the semicircle obtained. It is given that the wire used to create the semicircle was bent in the form of a square with an area $992.25\text{ c}{{\text{m}}^{2}}$ .
Hence, we can write the area of square of side a as
$\text{Area}={{a}^{2}}$

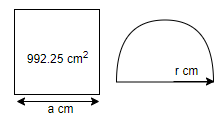
We know that the given area is $992.25\text{ c}{{\text{m}}^{2}}$ .Hence,
${{a}^{2}}=992.25$
Now, let us take the square root to get the side of the square.
$a=\sqrt{992.25}=31.5\text{cm}$
Let us find the perimeter of the square.
We know that perimeter of a square is given by
$\text{Perimeter}=4a$
Let us now substitute the values. We will get
$\text{Perimeter}=4\times 31.5=126\text{cm}$
It is given that the same wire is used to form a semicircle. Hence,
\[\text{Perimeter of the square }=\text{ circumference of the semicircle…}\left( \text{i} \right)\]
 We know that the circumference of a semicircle with radius r is given as
$\text{Circumference}=\pi r+2r$
Let us substitute this in (i). We will get
$\pi r+2r=126$
Let us take r outside from LHS. We will get
$r\left( \pi +2 \right)=126$
We can take the value of $\pi =\dfrac{22}{7}$ . Hence, the above equation becomes
$r\left( \dfrac{22}{7}+2 \right)=126$
Let us solve us. We will get
$r\left( \dfrac{36}{7} \right)=126$
Taking the constants to one side, we will get
$r=126\times \dfrac{7}{36}$
We can now solve this. We will get
$r=24.5\text{cm}$

Hence, the radius of the semicircle is 24.5 cm.

Note: You must know the formulas of different shapes starting from perimeter to the area. You may mistake the area of square as 4a and the perimeter of the square as ${{a}^{2}}$ . You may use the formula for circumference of a circle , that is, $2\pi r$ instead of $\pi r+2r$ .