Question

A well of diameter 150 cm has a stone parapet around it. If the length of the outer edge of the parapet is 660cm, then the width of the parapet is:
(a) 30cm
(b) 20cm
(c) 25cm
(d) 40cm

Answer 1

Hint: The diameter of the well is 150cm, so the diameter of the inner circle is 150cm. So, the inner radius is equal to 75cm, i.e., half of the inner diameter. Also, the length of the outer edge of the parapet is 660cm, i.e., the circumference of the outer circle is 660cm. We know that the circumference of the circle is given by $ 2\pi \left( radius \right) $ , so use this formula to get the outer radius. Finally find the difference between the inner and outer radius to get the answer.

Complete step-by-step answer:
To start with the question let us draw the diagram of the park with the road along its boundary for better visualisation.

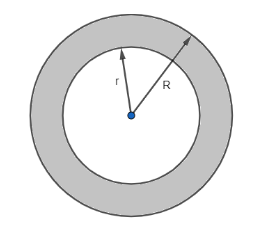
As it is given that the diameter of the well is 150cm, so the diameter of the inner circle is 150cm. So, the inner radius is equal to 75cm, i.e., half of the inner diameter.
 $ \therefore r=75cm $
Also, it is given that the length of the outer edge of the parapet is 660cm, i.e., the circumference of the outer circle is 660cm and we know that the circumference of the circle is given by $ 2\pi R $ .
 $ \begin{align}
  & \therefore 2\pi R=660 \\
 & \Rightarrow R=\dfrac{660}{2\pi } \\
\end{align} $
Now, if we put $ \pi =\dfrac{22}{7} $ , we get
 $ R=\dfrac{660\times 7}{2\times 22}=105cm $
Now, the width of the parapet is the difference of the outer and inner radius. So, the width of the parapet is:
 $ R-r=105-75=30cm $
So, the correct answer is “Option A”.

Note: The key to this question is to draw the correct diagram of the situation given in the question, as once you have drawn the diagram, we just have to put the formula of circumference of circle and find the difference of the two radii to get the answer. Also, be careful about the calculation part as there is a high chance of making a mistake in the calculation part.