Question

A wall has to be built with length 8m, thickness 3m and height 5m. Find the volume of the wall in cubic cm.
\[\left( a \right)520000000c{{m}^{3}}\]
\[\left( b \right)360000000c{{m}^{3}}\]
\[\left( c \right)210540000c{{m}^{3}}\]
\[\left( d \right)120000000c{{m}^{3}}\]

Answer 1

Hint: We are given the dimension of the wall as \[8\times 3\times 5.\] The wall is the same as the cuboid. So, we will find the volume of the cuboid (wall) using the formula \[V=L\times B\times H.\] The dimension we have is in meters. So the volume will come in \[{{m}^{3}}.\] Then, we will convert the volume in \[c{{m}^{3}}\] using the scale \[1{{m}^{3}}=1000000c{{m}^{3}}\] and unitary method.

Complete step-by-step solution:
We are given that the wall has a length of 8m, thickness 3m, and height 5m.

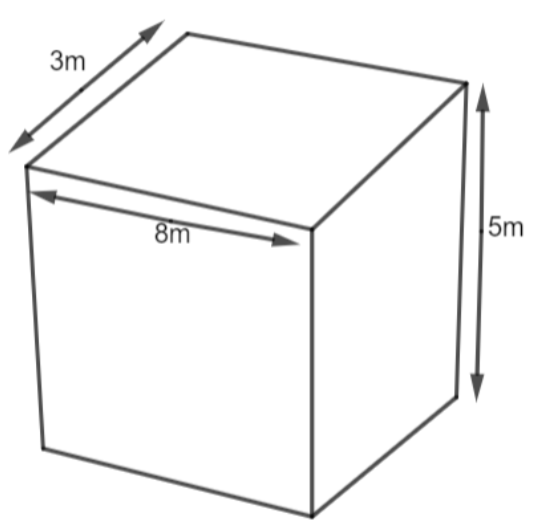
We know that the wall is in the shape of a cuboidal box. We have the length of the wall as 8m, thickness as 3m, and height as 5m. This means that we are given the length of the cuboid as 8m, the width of the cuboid as 3m, and the height of the cuboid as 5m.
The volume is now the same as the volume of the cuboid. We know that the volume of the cuboid is given as \[\text{Volume}=L\times B\times H.\]
We have L = 8, B = 3 and H = 5. So, the volume of the cuboid will be
\[\text{Volume of Cuboid}=8\times 3\times 5\]
\[\Rightarrow \text{Volume of Cuboid}=120{{m}^{3}}\]
So, we get the volume of the cuboid as \[120{{m}^{3}}.\] This means that the volume of the wall is \[120{{m}^{3}}.\]
Now, we need our final solution in \[c{{m}^{3}}.\] So, we will convert the volume of the wall from \[{{m}^{3}}\] to \[c{{m}^{3}}.\]
We know that,
\[1{{m}^{3}}=1000000c{{m}^{3}}\]
So by using the unitary method, we have,
\[120{{m}^{3}}=120\times 1000000c{{m}^{3}}=120000000c{{m}^{3}}\]
So, we get our final volume of the wall in \[c{{m}^{3}}\] as \[120000000c{{m}^{3}}.\]
Hence, option (d) is the right answer.

Note: We can also convert the dimension in the initial stage, but it will make our calculation a bit lengthy and complex. Here, \[1{{m}^{3}}=1000000c{{m}^{3}}\] because we know that 1m = 100 cm. So,
\[{{\left( 1m \right)}^{3}}={{\left( 100cm \right)}^{3}}\]
Multiplying 3 times to solve the cube, we get,
\[\Rightarrow 1{{m}^{3}}=100\times 100\times 100c{{m}^{3}}\]
\[\Rightarrow 1{{m}^{3}}=1000000c{{m}^{3}}\]